已知在三角形中∠C=90°，AC=3，BC=4，则△ABC的内切圆的面积是 ．
【答案】
分析：首先求出AB的长，再连圆心和各切点，利用切线长定理用半径表示AF和BF，而它们的和等于AB，得到关于r的方程，求出圆的面积即可．
解答：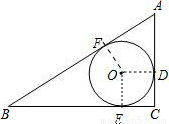
解：连OD，OE，OF，如图，设半径为r．则OE⊥BC，OF⊥AB，OD⊥AC，CD=r．
∵∠C=90°，BC=4，AC=3，
∴AB=5，
∴BE=BF=4-r，AF=AD=3-r，
∴4-r+3-r=5，
∴r=1．
∴△ABC的内切圆的面积是：π×1
2=π，
故答案为：π．
点评：此题主要考查了勾股定理以及直角三角形内切圆半径求法等知识，熟练掌握切线长定理和勾股定理．此题让我们记住一个结论：直角三角形内切圆的半径等于两直角边的和与斜边的差的一半．实际上直角三角形外接圆的半径等于斜边的一半．
