Question

在平面直角坐标系XOY中，有A（3，2），B （﹣1，﹣4 ），P是X轴上的一点，Q是Y轴上的一点，若以点A，B，P，Q四个点为顶点的四边形是平行四边形，则Q点的坐标是　　　　　　．

Answer 1

　（0，﹣6）或（0，﹣2）或（0，6）　．

【考点】平行四边形的判定；坐标与图形性质．

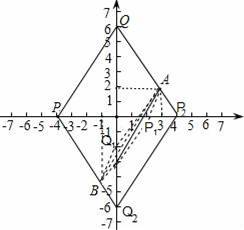
【分析】如图，当AB为边，①当四边形ABQ₂P₂是平行四边形，所以AB=P₂Q₂，AP₂=BQ₂，②当四边形QPBA是平行四边形，所以AB=PQ，QA=PB，当AB为对角线，即当四边形P₁AQ₁B是平行四边形，所以AP₁=Q₁B，AQ₁=BP₁，结合图形分别得出即可．

【解答】解：如图所示，

当AB为边，①即当四边形ABQ₂P₂是平行四边形，所以AB=P₂Q₂，AP₂=BQ₂，

∴Q₂点的坐标是：（0，﹣6），

②当四边形QPBA是平行四边形，所以AB=PQ，QA=PB，

∴Q点的坐标是：（0，6），

当AB为对角线，即当四边形P₁AQ₁B是平行四边形，所以AP₁=Q₁B，

AQ₁=BP₁，

∴Q₁点的坐标是：（0，﹣2）．

故答案为：（0，﹣6）或（0，﹣2）或（0，6）．

【点评】此题考查了平行四边形的性质：平行四边形的对边平行且相等，结合AB的长分别确定P，Q的位置是解决问题的关键．