
已知动点P以每秒2cm的速度沿如图所示的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
(1)如图甲,BC的长是多少?图形面积是多少?
(2)如图乙,图中的a是多少?b是多少?
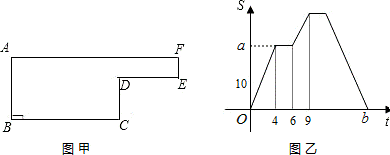
解:(1)已知当P在BC上时,以AB为底的高在不断增大,到达点C时,开始不变,由第二个图得,
P在BC上移动了4秒,那么BC=4×2=8cm.
在CD上移动了2秒,CD=2×2=4cm,
在DE上移动了3秒,DE=3×2=6cm,而AB=6cm,
那么EF=AB﹣CD=2cm,需要移动2÷2=1秒.
AF=CB+DE=14cm.需要移动14÷2=7秒,
S图形=AB×BC+DE×EF=6×8+6×2=60cm2.
(2)由图得,a是点P运行4秒时△ABP的面积,
∴S△ABP=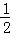 ×6×8=24,
×6×8=24,
b为点P走完全程的时间为:t=9+1+7=17s.
答:(1)故BC长是8cm,图形面积是60cm2;
(2)图中的a是24,b是17.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
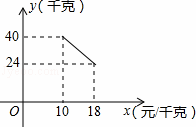
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
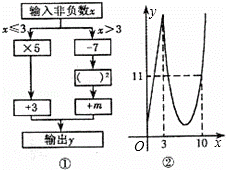
某同学根据图①所示的程序计算后,画出了图②中y与x之间的函数图象.
(1)当0≤x≤3时,y与x之间的函数关系式为 ;
(2)当x>3时,求出y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
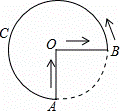
世界文化遗产“华安二宜楼”是一座圆形的土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB也匀速走到点B,紧接着沿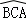 回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )
回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )
A. 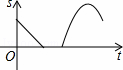 B.
B.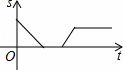 C.
C.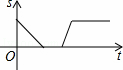 D.
D. 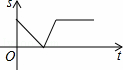
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com