解:(1)若四边形AECF为平行四边形,
∴AO=OC,EO=OF,
∵四边形ABCD为平行四边形,
∴BO=OD=6cm,
∴EO=6-t,OF=2t,
∴6-t=2t,
∴t=2s,
∴当t为2秒时,四边形AECF是平行四边形;
(2)①若四边形AECF是菱形,
∴AC⊥BD,
∴AO
2+BO
2=AB
2,
∴AB=
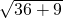
=
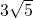
;
②不可以.
若是矩形,EF=AC,
∴6-t+2t=6,
∴t=0,
则此时E在点B上,F在O上,
显然四边形AECF不是矩形.
分析:(1)若是平行四边形,所以BD=12cm,则B0=DO=6cm,故有6-1t=2t,即可求得t值;
(2)①若是菱形,则AC垂直于BD,即有AO
2+BO
2=AB
2,故AB可求;
②若是矩形,EF=AC,则此时E在O上,所以四边形AECF不可以是矩形.
点评:本此综合考查平行四边形的判定和菱形的判定.考查学生综合运用数学知识的能力.

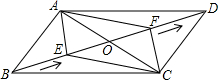 B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.
B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.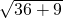 =
=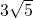 ;
;

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案