
分析 如图,过点A作DE∥B1C1,交直线PB1于D,交直线PC1于E.连接BQ,设AB交B1C1于F.首先证明AB=AD同理可得AC=AE,由AB=AC,推出AD=AE,再根据B1C1∥ED,得$\frac{{A}_{1}{B}_{1}}{AD}$=$\frac{P{A}_{1}}{PA}$=$\frac{{A}_{1}{C}_{1}}{AE}$,由此即可证明.
解答 证明:如图,过点A作DE∥B1C1,交直线PB1于D,交直线PC1于E.连接BQ,设AB交B1C1于F.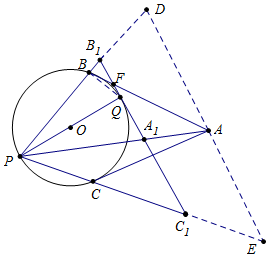
∴FB=FQ,∠FBQ=∠FQB,
∵PQ是直径,
∴∠PBQ=∠QBB1=90°,
∴∠FBB1+∠FBQ=90°,∠BB1Q+∠BQB1=90°,
∴∠FBB1=∠FB1B,
∵DE∥B1C1,
∴∠ADB=∠BB1Q=∠ABD,
∴AB=AD,同理可证AC=AE,
∵AB,AC是切线,
∴AB=AC,
∴AD=AE,
∵B1C1∥ED,
∴$\frac{{A}_{1}{B}_{1}}{AD}$=$\frac{P{A}_{1}}{PA}$=$\frac{{A}_{1}{C}_{1}}{AE}$,
∴A1B1=A1C1.
点评 本题考查了切线的性质、平行线分线段成比例定理、切线长定理等知识,解题的关键是学会添加常用辅助线,构造平行线利用平行线分线段成比例定理解决问题,题目比较难,有一定的挑战性.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
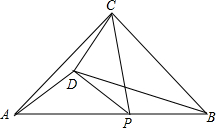 如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.
如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
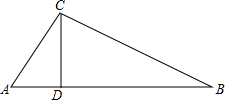 如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.
如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,粮仓的顶部是圆锥形,此圆锥底面的直径为12m,母线长为8m,为防雨需在粮仓的顶部铺上油毡,若铺油毡的费用为30元/m2,则共需花4520元.(π取3.14,精确到10元)
如图,粮仓的顶部是圆锥形,此圆锥底面的直径为12m,母线长为8m,为防雨需在粮仓的顶部铺上油毡,若铺油毡的费用为30元/m2,则共需花4520元.(π取3.14,精确到10元)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com