
 如图,已知⊙O的半径为l,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点.
如图,已知⊙O的半径为l,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点.分析 (1)连接BD,由ED为圆O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由BCOE为平行四边形,得到BC与OE平行,且BC=OE=1,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD的长即可;
(2)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线.
解答 解:(1)如图,连接BD,
∵DE是直径,
∴∠DBE=90°,
如果四边形BCOE为平行四边形,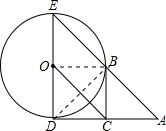
∴BC∥OE,BC=OE=1,
在Rt△ABD中,C为AD的中点,
∴BC=$\frac{1}{2}$AD=1,
则AD=2,
∴当AD=2时,四边形BCOE为平行四边形,
故答案为:2;
(2)是,理由如下:
如图,连接OB.
∵BC∥OD,BC=OD,
∴四边形BCDO为平行四边形,
∵AD为圆O的切线,
∴OD⊥AD,
∴四边形BCDO为矩形,
∴OB⊥BC,
则BC为圆O的切线.
点评 此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 周末数学老师布置了实践作业,小明来到一条河岸边的一段,想测量河的宽度.如图所示,河岸AB上有一排树,相邻两棵树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得α=26.6°,然后沿河岸走50米到达N点,测得β=63.4°.请你根据这些数据帮小明算出河的宽FG(结果保留整数).(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.5,sin63.4°≈0.89,cos63.4°≈0.45,tan63.4°≈2)
周末数学老师布置了实践作业,小明来到一条河岸边的一段,想测量河的宽度.如图所示,河岸AB上有一排树,相邻两棵树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得α=26.6°,然后沿河岸走50米到达N点,测得β=63.4°.请你根据这些数据帮小明算出河的宽FG(结果保留整数).(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.5,sin63.4°≈0.89,cos63.4°≈0.45,tan63.4°≈2)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
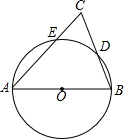 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD.∠C=70°,以下四个结论中错误的是( )
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD.∠C=70°,以下四个结论中错误的是( )| A. | AC=AB | B. | $\widehat{DE}$=$\widehat{BD}$ | C. | ∠A=45° | D. | $\frac{CE}{CD}$=$\frac{CB}{CA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABE中,∠A=Rt∠,AB=5,BE=13,以点B为旋转中心,将BE顺时针旋转90°至BC,过点C作CD∥AB分别交AE、BE于点D、F,则DF的长为$\frac{35}{12}$.
如图,在Rt△ABE中,∠A=Rt∠,AB=5,BE=13,以点B为旋转中心,将BE顺时针旋转90°至BC,过点C作CD∥AB分别交AE、BE于点D、F,则DF的长为$\frac{35}{12}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com