练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1）如图1是一个重要公式的几何解释．请你写出这个公式；

    （2）如图2，，，且三点共线．试证明；

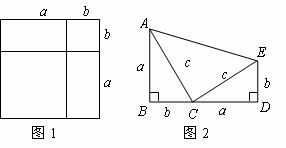
    （3）伽菲尔德（，1881年任美国第20届总统）利用（1）中的公式和图2证明了勾股定理（1876年4月1日，发表在《新英格兰教育日志》上），现请你尝试该证明过程．

    解：（1）这个公式为．

    （2），．

    ．

    由于共线，

    所以

    ．

    （3）梯形的面积为

    ；

    另一方面，梯形可分成三个直角三角形，其面积又可以表示成

    ．

    所以，．

    即．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    16、小明与小华在玩一个掷飞镖游戏，如图甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小明胜，否则小华胜（没有掷中靶或掷到边界线时重掷）．
    （1）不考虑其他因素，你认为这个游戏公平吗说明理由；
    （2）请你在图乙中，设计一个不同于图甲的方案，使游戏双方公平．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1是一个小正方体的侧面展开图，小正方体从图2所示的位置依次翻到第1格、第2格、第3格，这时小正方体朝上面的字是（　　）

    查看答案和解析>>

    科目：初中数学 来源：2011届北京市昌平区初三第二学期第一次统一练习数学卷 题型：解答题

    (6分)小刚与小华在玩一个掷飞镖游戏，如图甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小刚胜，否则小华胜（没有掷中靶或掷到边界时重掷）。

    （1）不考虑其他因素，你认为这个游戏对双方公平吗？说明理由；

    （2）请你在图乙中，设计一个不同于图甲的方案，使游戏对双方公平。

     

    查看答案和解析>>

    科目：初中数学 来源：第2章《简单事件的概率》中考题集（31）：2.3 概率的简单应用（解析版） 题型：解答题

    小明与小华在玩一个掷飞镖游戏，如图甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小明胜，否则小华胜（没有掷中靶或掷到边界线时重掷）．
    （1）不考虑其他因素，你认为这个游戏公平吗？说明理由；
    （2）请你在图乙中，设计一个不同于图甲的方案，使游戏双方公平．

    查看答案和解析>>

    科目：初中数学 来源：第25章《概率初步》中考题集（35）：25.2 用列举法求概率（解析版） 题型：解答题

    小明与小华在玩一个掷飞镖游戏，如图甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小明胜，否则小华胜（没有掷中靶或掷到边界线时重掷）．
    （1）不考虑其他因素，你认为这个游戏公平吗？说明理由；
    （2）请你在图乙中，设计一个不同于图甲的方案，使游戏双方公平．

    查看答案和解析>>

    同步练习册答案