

分析 (1)根据题意得到规律即可得到结论;
(2)根据题意得到规律即可得到结论;
(3)根据规律即可得到结论.
解答 解:(1)根据上面的规律第5个式子为:3×(12+22+32+42+52)=11(1+2+3+4+5);
故答案为:3×(12+22+32+42+52)=11(1+2+3+4+5);
(2)根据上面的规律第n个式子为:3(12+22+32+…+n2)=(2n+1)(1+2+3+4+…+n);
故答案为:3(12+22+32+…+n2)=(2n+1)(1+2+3+4+…+n);
(3)∵12+32=10=$\frac{1}{3}$×2(4×22-1),12+32+52=35=$\frac{1}{3}$×3×(4×32-1),12+32+52+72=$\frac{1}{3}$×4×(4×42-1),…,
∴12+32+52+…+(2n+1)2=$\frac{1}{3}$(n+1)•[4×(n+1)2-1],
∴12+32+52+…+392=$\frac{1}{3}$(19+1)[4×(19+1)2-1]=33540.
故答案为:33540.
点评 本题考查了数字的变化类,解此题的关键是找出规律直接解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
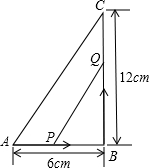 如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC 以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC 以2cm/s的速度移动,如果P、Q分别从A、B同时出发:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
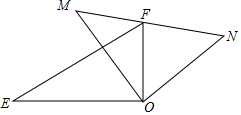 如图,一副三角板的两个直角顶点重合在一起.
如图,一副三角板的两个直角顶点重合在一起.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
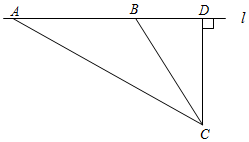 某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com