
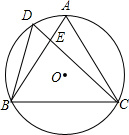
 如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )
如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AE•BE=CE•ED;③CA2=CE•CD;④CD=BD+AD.其中正确的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 连接AD,根据等边三角形的性质得到∠BAC=∠ABC=60°,由圆周角定理得到∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,于是得到∠BDC=∠ADC=60°,故①正确;根据圆周角定理得到∠D=∠A,∠ABD=∠ACD,推出△BDE∽△ACE,根据相似三角形的性质即可得到AE•BE=CE•ED;故②正确;由于∠ADC=∠EAC=60°,∠ACE=∠ACD,得到△ACD∽△ACE,根据相似三角形的性质得到CA2=CE•CD;故③正确;在CD上截取CF=BD,通过△ABD≌△ACF,得到AD=AF,推出△ADF是等边三角形,得到DF=AD,等量代换即可得到结论.
解答 解:连接AD,∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,
∴∠BDC=∠ADC=60°,故①正确;
∵∠D=∠A,∠ABD=∠ACD,
∴△BDE∽△ACE,
∴$\frac{BE}{CE}=\frac{DE}{AE}$,
∴AE•BE=CE•ED;故②正确;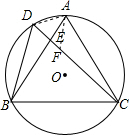
∵∠ADC=∠EAC=60°,∠ACE=∠ACD,
∴△ACD∽△ACE,
∴$\frac{AC}{CD}=\frac{CE}{AC}$,
∴CA2=CE•CD;故③正确;
在CD上截取CF=BD,
在△ABD与△ACF中,$\left\{\begin{array}{l}{BD=CF}\\{∠ABD=∠ACF}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACF,
∴AD=AF,
∵∠ADC=60°,
∴△ADF是等边三角形,
∴DF=AD,
∵CD=CF+DF,
∴CD=BD+AD.故④正确.
故选A.
点评 此题考查了圆周角定理,全等三角形的判定和性质,等边三角形的性质,相似三角形的判定与性质,熟练掌握定理及性质是解本题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
 已知一次函数y=kx+b的图象(如图所示),那么正比例函数y=kx和反比例函数y=$\frac{b}{x}$在同一坐标系的图象可能是( )
已知一次函数y=kx+b的图象(如图所示),那么正比例函数y=kx和反比例函数y=$\frac{b}{x}$在同一坐标系的图象可能是( )| A. |  | B. | 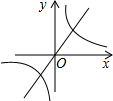 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,近几年我国的雾霾越来越严重,汽车尾气是造成雾霾的重要原因之一.为减少雾霾,黎明响应“绿色出行”的号召,上班由自驾车改为乘坐地铁.已知黎明家距离上班地点16千米,他乘坐地铁平均每小时走的路程比他自驾车平均每小时行驶的路程的2倍还多8千米,他从家出发到上班地点,乘坐地铁所用时间是自驾车所用时间的$\frac{5}{12}$.问黎明乘坐地铁上班平均每小时走多少千米?
如图,近几年我国的雾霾越来越严重,汽车尾气是造成雾霾的重要原因之一.为减少雾霾,黎明响应“绿色出行”的号召,上班由自驾车改为乘坐地铁.已知黎明家距离上班地点16千米,他乘坐地铁平均每小时走的路程比他自驾车平均每小时行驶的路程的2倍还多8千米,他从家出发到上班地点,乘坐地铁所用时间是自驾车所用时间的$\frac{5}{12}$.问黎明乘坐地铁上班平均每小时走多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com