
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C、D、E三点不在同一直线上时,以ED、EC我邻边作?ECFD,设点D运动的时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C、D、E三点不在同一直线上时,以ED、EC我邻边作?ECFD,设点D运动的时间为t(秒).分析 (1)分两种情形分别求出CE的长即可;
(2)求出点F落在AB或AC上的时间即可解决问题.
(3)分两种情形求解即可;
(4)分四种情形列出方程求解即可解决问题;
解答 解:(1)由题意,BE=2t,
当点E与点C重合时,2t=3,
∴t=$\frac{3}{2}$,
当点D与点C重合时,t=4.
∴当0≤t<$\frac{3}{2}$时,CE=BC-BE=3-2t.
当$\frac{3}{2}$≤t≤4时,CE=BE-BC=2t-3.
(2)当F落在AB上时,tanA=$\frac{DF}{AD}$=$\frac{BC}{AC}$,
∴$\frac{2t-3}{t}$=$\frac{3}{4}$,
∴t=$\frac{12}{5}$,
当点F落在AC边上时,点E与点C重合,
∴t=$\frac{3}{2}$,
∴当点F落在△ABC的内部时,$\frac{3}{2}$<t<$\frac{12}{5}$.
(3)当0≤t<$\frac{3}{2}$时,S=EC•DC=(3-2t)(4-t)=2t2-11t+12.
当$\frac{3}{2}$<t<4时,S=EC•DC=(2t-3)(4-t)=-2t2+11t-12,
综上所述,S=$\left\{\begin{array}{l}{2{t}^{2}-11t+12}&{(0≤t<\frac{3}{2})}\\{-2{t}^{2}+11t-12}&{(\frac{3}{2}<t<4)}\end{array}\right.$.
(4)由题意DC=2DF或DF=2DC,
则有4-t=2(3-2t),解得t=$\frac{2}{3}$,此时S=$\frac{50}{9}$,
或3-2t=2(4-t),无解,不存在,
或4-t=2(2t-3),解得t=2,此时S=2,
或2t-3=2(4-t),解得t=$\frac{11}{4}$,此时S=$\frac{25}{8}$
∴?ECFD的面积为$\frac{50}{9}$或2或$\frac{25}{8}$.
点评 本题考查四边形综合题、平行四边形的性质、锐角三角函数、一元一次方程的应用、二次函数的应用等知识,解题的关键是学会用分类讨论是思想思考问题,学会构建方程解决问题,属于中考压轴题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
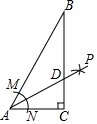 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )| A. | AD平分∠BAC | B. | S△DAC:S△ABC=1:2 | ||
| C. | 点D在线段AB的垂直平分线上 | D. | ∠ADC=60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
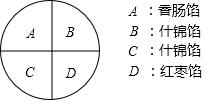 大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.
大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
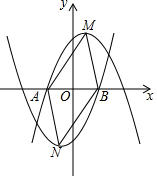 如图,在平面直角坐标系中,抛物线y=-(x-h)2+2(h>0)的顶点为M,与x轴负半轴的交点为A,抛物线y=(x+h)2-2的顶点为N,与x轴正半轴的交点为B,若AB=2h,则四边形MANB的面积为2$\sqrt{2}$.
如图,在平面直角坐标系中,抛物线y=-(x-h)2+2(h>0)的顶点为M,与x轴负半轴的交点为A,抛物线y=(x+h)2-2的顶点为N,与x轴正半轴的交点为B,若AB=2h,则四边形MANB的面积为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
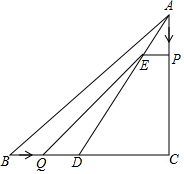 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在边BC上,且CD=3cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点运动;点Q以1.25cm/s的速度沿BC向终点C运动,过点P作PE∥BC交AD于点E,连接EQ,设动点运动时间为ts(0<t<4).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在边BC上,且CD=3cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点运动;点Q以1.25cm/s的速度沿BC向终点C运动,过点P作PE∥BC交AD于点E,连接EQ,设动点运动时间为ts(0<t<4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
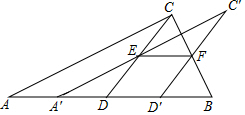 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
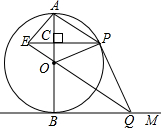 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com