

���� ��1����OA=m����tan��OAC=3���ó�OC=3OA=3m���ɡ�OBC�ǵ���ֱ�������εó�OB=OC=3m������AB=OA+OB=4m=4�����m=1���õ�A��-1��0����B��3��0����C��0��3���������ô���ϵ����������������ߵĽ���ʽ��
��2���������䷽����������ߵĶ���D�����꣬�ټ���ó�BC2+CD2=BD2�����ݹ��ɶ������涨���õ���DCB=90�㣬��tan��CDB=3���õ���CDB=��OAC�����ݵȽǵ������ȵó���CBD=��OCA����ôsin����OBD-��OCA��=sin��OBC=sin45��=$\frac{\sqrt{2}}{2}$��
��3���ٸ����۵������ʵó�CE=C��E����AE=n����tan��OAC=3���õ�CE=C��E=3n����ôCE=$\frac{3\sqrt{10}}{4}$����֤����CEF�ס�CBA���������������ζ�Ӧ�߳ɱ������EF=$\sqrt{5}$��
�����ɡ�CEF�ס�CBA���������������ζ�Ӧ�߳ɱ������CF=$\frac{5\sqrt{2}}{4}$����ô���F��$\frac{5}{4}$��$\frac{7}{4}$����E��-$\frac{3}{4}$��$\frac{3}{4}$�������ɡ�C��EA�ס�COA�����C��A=$\frac{5}{2}$����ôC�䣨$\frac{3}{2}$��0����Ȼ�����ƽ���ı��εĶԽ�����ƽ����õ�P�����꣮
��� �⣺��1����OA=m��
��tan��OAC=3��
��OC=3OA=3m��
�ߡ�OBC=45�㣬��COB=90�㣬
���OCB=45�㣬
��OB=OC=3m��
��AB=OA+OB=4m=4����m=1��
��A��-1��0����B��3��0����C��0��3����
���辭��A��B��C�����������Ϊy=a��x+1����x-3����
����0��3��������ʽ����3=-3a�����a=-1��
��������ߵĽ���ʽΪy=-x2+2x+3��
��2����y=-x2+2x+3=-��x-1��2+4��
�ඥ��DΪ��1��4����
��B��3��0����C��0��3����
��CD=$\sqrt{2}$��BC=3$\sqrt{2}$��BD=2$\sqrt{5}$��
��BC2+CD2=BD2��
���DCB=90�㣬��tan��CDB=3��
���CDB=��OAC������CBD=��OCA��
��sin����OBD-��OCA��=sin����OBD-��CBD��=sin��OBC=sin45��=$\frac{\sqrt{2}}{2}$��
��3����������ɵ�CE=C��E����AE=n��
��tan��OAC=3��
��CE=C��E=3n����CE=$\frac{3}{4}$AC=$\frac{3\sqrt{10}}{4}$��
�ߡ�CEF=��CBA=45�㣬��ECF=��BCA��
���CEF�ס�CBA��
��$\frac{EF}{AB}$=$\frac{CE}{BC}$����$\frac{EF}{4}$=$\frac{\frac{3\sqrt{10}}{4}}{3\sqrt{2}}$��
��EF=$\sqrt{5}$�� �ڡߡ�CEF�ס�CBA��
�ڡߡ�CEF�ס�CBA��
��$\frac{CF}{CA}$=$\frac{CE}{BC}$����$\frac{CF}{\sqrt{10}}$=$\frac{\frac{3\sqrt{10}}{4}}{3\sqrt{2}}$��
��CF=$\frac{5\sqrt{2}}{4}$��
��F��$\frac{5}{4}$��$\frac{7}{4}$����E��-$\frac{3}{4}$��$\frac{3}{4}$����
�ߡ�C��EA�ס�COA��
��$\frac{C��A}{CA}$=$\frac{C��E}{CO}$��$\frac{C��A}{\sqrt{10}}$=$\frac{\frac{3\sqrt{10}}{4}}{3}$��
��C��A=$\frac{5}{2}$��
��C�䣨$\frac{3}{2}$��0����
��E��F��C�䡢PΪ������ı���Ϊƽ���ı���ʱ������������������ۣ�
��EFΪ�Խ���ʱ��C��P��EF���е��غϣ����P������Ϊ��-1��$\frac{5}{2}$����
��EFΪ��ʱ�����FP��C��E���е��غϣ����P������Ϊ��-$\frac{1}{2}$��-1�������EP��C��F���е��غϣ����P������Ϊ��$\frac{7}{2}$��1����
������������P��������-1��$\frac{5}{2}$������-$\frac{1}{2}$��-1������$\frac{7}{2}$��1����
���� �����Ƕ��κ������ۺ����ͣ������漰��������Ǻ����Ķ��壬����ֱ�������ε��ж������ʣ�����ϵ��������κ����Ľ���ʽ�������߶�������������ɶ������涨�����۵������ʣ����������ε��ж������ʣ�ƽ���ı��ε����ʵ�֪ʶ���ۺ��Խ�ǿ����һ���Ѷȣ��������ν�ϡ����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
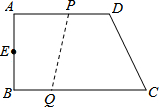 ��֪����ͼ��������ABCD�У�AD��BC����B=90�㣬AB=14cm��AD=18cm��BC=21cm����P�ӵ�A��ʼ��AD�����D��1cm/����ٶ��ƶ�����Q�ӵ�C��ʼ��CB�����B��2cm/����ٶ��ƶ������P��Q�ֱ��A��Cͬʱ���������ƶ���ʱ��Ϊt��
��֪����ͼ��������ABCD�У�AD��BC����B=90�㣬AB=14cm��AD=18cm��BC=21cm����P�ӵ�A��ʼ��AD�����D��1cm/����ٶ��ƶ�����Q�ӵ�C��ʼ��CB�����B��2cm/����ٶ��ƶ������P��Q�ֱ��A��Cͬʱ���������ƶ���ʱ��Ϊt���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9.001��10-3 | B�� | -9.001��10-3 | C�� | 0.9001��10-3 | D�� | -0.9001��10-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 98��104 | B�� | 9.8��105 | C�� | 9.8��106 | D�� | 0.98��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com