
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.

(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)设点D的坐标为(4,m)(m>0),则点A的坐标为(4,3+m),由点A的坐标表示出点C的坐标,根据C、D点在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出关于k、m的二元一次方程,解方程即可得出结论;
(2)由m的值,可找出点A的坐标,由此即可得出线段OB、AB的长度,通过解直角三角形即可得出结论;
(3)由m的值,可找出点C、D的坐标,设出过点C、D的一次函数的解析式为y=ax+b,由点C、D的坐标利用待定系数法即可得出结论.
试题解析:(1)设点D的坐标为(4,m)(m>0),则点A的坐标为(4,3+m),∵点C为线段AO的中点,∴点C的坐标为(2,![]() ).
).
∵点C、点D均在反比例函数![]() 的函数图象上,∴
的函数图象上,∴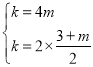 ,解得:
,解得:![]() ,∴反比例函数的解析式为
,∴反比例函数的解析式为![]() .
.
(2)∵m=1,∴点A的坐标为(4,4),∴OB=4,AB=4.
在Rt△ABO中,OB=4,AB=4,∠ABO=90°,∴OA=![]() =
=![]() ,cos∠OAB=
,cos∠OAB=![]() =
=![]() .
.
(3))∵m=1,∴点C的坐标为(2,2),点D的坐标为(4,1).
设经过点C、D的一次函数的解析式为y=ax+b,则有![]() ,解得:
,解得: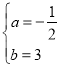 ,∴经过C、D两点的一次函数解析式为
,∴经过C、D两点的一次函数解析式为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】

A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
查看答案和解析>>
科目:初中数学 来源: 题型:
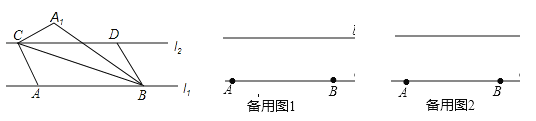
【题目】已知:直线l1与直线l2平行,且它们之间的距离为2,A、B是直线l1上的两个定点,C、D是直线l2上的两个动点(点C在点D的左侧),AB=CD=5,连接AC、BD、BC,将△ABC沿BC折叠得到△A1BC.
(1)求四边形ABDC的面积.
(2)当A1与D重合时,四边形ABDC是什么特殊四边形,为什么?
(3)当A1与D不重合时:①连接A1、D,求证:A1D∥BC;②若以A1,B,C,D为顶点的四边形为矩形,且矩形的边长分别为a,b,求(a+b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为计算简便,把(-2.4)-(-4.7)-(+0.5)+(+3.4)+(-3.5)写成省略加号的和的形式,并按要求交换加数的位置正确的是( ).
A. -2.4+3.4-4.7-0.5-3.5
B. -2.4+3.4+4.7+0.5-3.5
C. -2.4+3.4+4.7-0.5-3.5
D. -2.4+3.4+4.7-0.5+3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①所有的有理数都能用数轴上的点表示;
②符号不同的两个数互为相反数;
③有理数分为正数和负数;
④两数相减,差一定小于被减数;
⑤两数相加,和一定大于任何一个加数.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳远队准备从甲、乙、丙、丁4名运动员中选取成绩好且稳定的一名选手参赛,经测试,他们的成绩如下表,综合分析应选
成绩 | 甲 | 乙 | 丙 | 丁 |
平均分(单位:米) | 6.0 | 6.1 | 5.5 | 4.6 |
方差 | 0.8 | 0.2 | 0.3 | 0.1 |
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
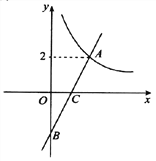
【题目】如图在平面直角坐标系xOy中,函数![]() (
(![]() )的图象与一次函数
)的图象与一次函数![]() 的图象的交点为A(m,2).
的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)观察图像直接写出使得![]() 的
的![]() 的取值范围;
的取值范围;
(3)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com