梯形的两腰分别是4和6,上底为2,则下底x的取值范围是________.
4<x<12
分析:过D作DE∥AB交BC于E,得出平行四边形ABED,推出BE=AD=2,AB=DE=6,CE=x-2,在△DEC中,由三角形的三边关系定理得出6-4<x-2<6+4,求出即可.
解答:
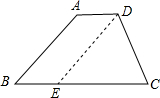
过D作DE∥AB交BC于E,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴BE=AD=2,AB=DE=6,
CE=x-2,
在△DEC中,由三角形的三边关系定理得:6-4<x-2<6+4,
解得:4<x<12.
故答案为:4<x<12.
点评:本题考查的知识点有梯形的性质、平行四边形的性质和判定、三角形的三边关系定理,解本题的关键是把梯形转化成平行四边形和三角形.
