
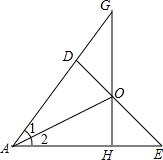
 已知:如图,OD⊥AD,OH⊥AE,DE交GH于O.
已知:如图,OD⊥AD,OH⊥AE,DE交GH于O.分析 (1)先根据角平分线的性质得:OD=OH,再证明△GDO≌△EHO,可得结论;
(2)先证明△GDO≌△EHO,得OD=OH,根据角平分线的逆定理得:AO平分∠DAH,则∠1=∠2.
解答 证明:(1)∵∠1=∠2,OD⊥AD,OH⊥AE,
∴OD=OH,∠ODG=∠OHE=90°,
在△GDO和△EHO中,
∵$\left\{\begin{array}{l}{∠ODG=∠OHE}\\{∠DOG=∠HOE}\\{OD=OH}\end{array}\right.$,
∴△GDO≌△EHO(AAS),
∴OG=OE;
(2)∵OD⊥AD,OH⊥AE,
∴∠ODG=∠OHE=90°,
在△GDO和△EHO中,
∵$\left\{\begin{array}{l}{∠ODG=∠OHE}\\{∠DOG=∠HOE}\\{OG=OE}\end{array}\right.$,
∴△GDO≌△EHO(AAS),
∴OD=OH,
∴O在∠DAH的角平分线上,
即AO平分∠DAH,
∴∠1=∠2.
点评 本题考查了全等三角形的性质和判定及角平分线性质定理,熟练掌握角平分线的性质是关键:①角的平分线上的点到角的两边的距离相等,②到一个角两边距离相等的点在这个角的平分线上;有时角平分线的性质得出的结论可以由全等得出,不过比较麻烦.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
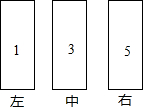 如图所示,三根音管被敲击时能依次发出“1”“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击这三根音管,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…).第2012拍时,听到相同的音,这个相同的音是3.
如图所示,三根音管被敲击时能依次发出“1”“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击这三根音管,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…).第2012拍时,听到相同的音,这个相同的音是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com