
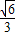 时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).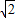 ≈1.414;
≈1.414;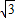 ≈1.732;
≈1.732;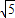 ≈2.236)
≈2.236)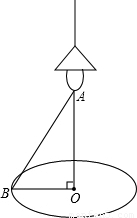
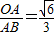 ,所以OA=
,所以OA=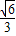 AB,然后根据勾股定理得OA2+OB2=AB2,且OB=60cm解得OA;
AB,然后根据勾股定理得OA2+OB2=AB2,且OB=60cm解得OA;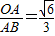 ,分别假设OA=
,分别假设OA= x,AB=3x,再有OB=60,根据勾股定理先求出x,再进而求出OA的长.
x,AB=3x,再有OB=60,根据勾股定理先求出x,再进而求出OA的长.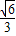 ,
,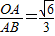 ,
,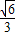 AB,
AB,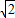 ≈85cm,
≈85cm, ,
,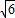 x,AB=3x(x>0),
x,AB=3x(x>0),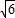 x)2+602=(3x)2
x)2+602=(3x)2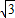 ,
,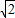 ≈85cm.
≈85cm.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《图形的旋转》(03)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(17)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2005年江苏省淮安市中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2005年江苏省淮安市中考数学试卷(课标卷)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com