
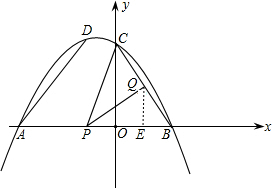
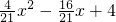 与x轴交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.动点P从A点出发沿线段AB以每秒
与x轴交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.动点P从A点出发沿线段AB以每秒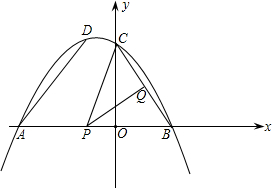 2个单位长度的速度向终点B运动;同时动点Q从B点出发沿线段BC以每秒1个单位长度的速度向终点C运动.设运动的时间为t秒.
2个单位长度的速度向终点B运动;同时动点Q从B点出发沿线段BC以每秒1个单位长度的速度向终点C运动.设运动的时间为t秒. 解:(1)∵抛物线y=-
解:(1)∵抛物线y=-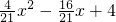 与x轴交于A,B两点(点A在点B的左侧),
与x轴交于A,B两点(点A在点B的左侧),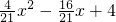 ,
,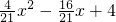 ,
,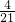 (x2+4x)+4,
(x2+4x)+4,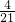 (x2+4x+4-4)+4,
(x2+4x+4-4)+4,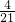 [(x+2)2-4]+4,
[(x+2)2-4]+4,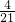 [(x+2)2+
[(x+2)2+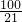 ,
,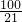 ),
),
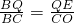 ,
,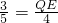 ,
, ×4×4=8,
×4×4=8, ×PB×2.4=4.8,
×PB×2.4=4.8, ,
,
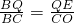 ,
,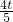 ,
,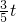 ,
, t,
t,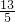 t,
t, 秒,
秒, ,
, PB=5-t,
PB=5-t, t,
t, t=5-t,
t=5-t, ,
, =10-2t,
=10-2t, ,
, ,t=
,t= ,t=
,t= ,时,△PQB为等腰三角形.
,时,△PQB为等腰三角形.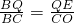 ,
,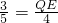 ,即可得出QE的长,进而求出S△PCB=
,即可得出QE的长,进而求出S△PCB= ×4×4=8,S△PQB的面积即可得出答案;
×4×4=8,S△PQB的面积即可得出答案;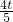 ,BE=
,BE=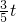 ,OE=3-
,OE=3- t,PO=7-2t,进而求出即可;
t,PO=7-2t,进而求出即可;

 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
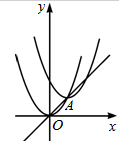 (2013•甘井子区一模)如图,抛物线y=x2与直线y=x交于A点,沿直线y=x平移抛物线,使得平移后的抛物线顶点恰好为A点,则平移后抛物线的解析式是( )
(2013•甘井子区一模)如图,抛物线y=x2与直线y=x交于A点,沿直线y=x平移抛物线,使得平移后的抛物线顶点恰好为A点,则平移后抛物线的解析式是( )查看答案和解析>>
科目:初中数学 来源: 题型:
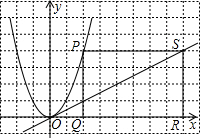 如图,抛物线y=x2与直线y=
如图,抛物线y=x2与直线y=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2013届北京市顺义区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知:如图,抛物线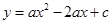 (
( )与
)与 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点 ,
, ,点
,点 的坐标为(4,0).
的坐标为(4,0).
(1) 求该抛物线的解析式;
(2) 点 是线段
是线段 上的动点,过点
上的动点,过点 作
作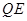 ∥
∥ ,交
,交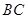 于点
于点 ,连接
,连接 . 当
. 当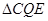 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标;
(3)若平行于 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点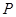 ,与直线
,与直线 交于点
交于点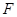 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点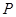 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2010年江西省中等学校招生考试数学试卷样卷(解析版) 题型:解答题
 与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com