
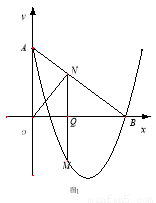
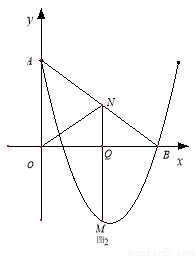
如图1,在平面直角坐标系中,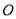 为坐标原点.直线
为坐标原点.直线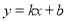 与抛物线
与抛物线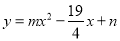 同时经过
同时经过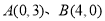 .
.

(1)求 的值.
的值.
(2)点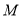 是二次函数图象上一点,(点
是二次函数图象上一点,(点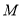 在
在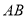 下方),过
下方),过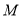 作
作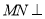
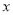 轴,与
轴,与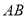 交于点
交于点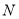 ,与
,与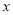 轴交于点
轴交于点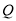 .求
.求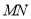 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点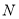 ,使
,使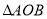 和
和 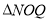 相似?若存在,求出
相似?若存在,求出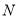 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
(1)m=1,n=3;(2)4;(3)N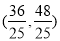 或N
或N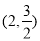 .
.
【解析】
试题分析:(1)应用待定系数法求抛物线的解析式中的m和n的值;
(2)求出一次函数解析式,联系点的坐标的几何意义表示线段MN的长,根据所列关系式求最大值;
(3)分两种情况讨论,当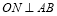 时,得到
时,得到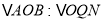 ,计算OQ和NQ的值,得点N的坐标;当N为AB中点时,得到
,计算OQ和NQ的值,得点N的坐标;当N为AB中点时,得到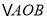 ∽
∽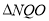 ,进而得到点N的坐标.
,进而得到点N的坐标.
试题解析:【解析】
(1)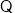 抛物线
抛物线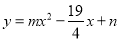 经过两点
经过两点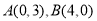 ,
,
∴ ,解得:
,解得: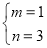 ,
,
所以m的值为1,n的值为3,此时二次函数的表达式为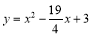 .
.
(2)把点A(0,3),点B(4,0)代入y=kx+b,得:
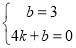 ,解得:
,解得: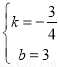 ,
,
∴经过A、B两点的一次函数的解析式为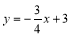 .
.
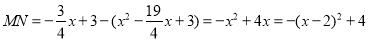 ,
,
∵0≤x≤4,∴ 当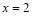 时,
时,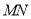 取得最大值为4.
取得最大值为4.
(3)存在.
①当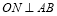 时,(如图1)
时,(如图1)
可证: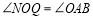 ,
,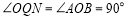 ,
,
∴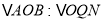 ,
,
∴ 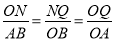 ,
,
∵OA=3,OB=4,
∴AB=5,
∵ON·AB=OA·OB,
∴ON=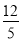 ,
,
∴NQ=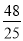 ,OQ=
,OQ=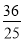 ,
,
∴N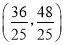 ;
;
②当N为AB中点时,(如图2)
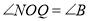 ,
,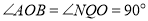
∴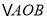 ∽
∽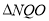 ,此时
,此时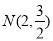 .
.
∴满足条件的N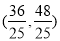 或N
或N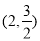 .
.
考点:1、待定系数法求解析式;2、图形与坐标;3、相似三角形的判定和性质.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源:2014-2015学年广东省广州学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
宿城区2 011年生产总值约185亿元,2013年生产总值约215亿元,求该区生产总值的年平均增长率。设宿城区生产总值的年平均增长率为x,则根据题意可列方程为___________________________。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃敦煌市九年级上学期期中检测数学试卷(解析版) 题型:选择题
某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份 平均每月的增长率为x,那么x满足的方程是( )
A、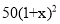 =182 B.50+50(1+x)+
=182 B.50+50(1+x)+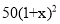 =182
=182
C、50(1+2x)=182 D.50+50(1+x)(1+2x)=182
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市密云县九年级第一学期期末考试数学试卷(解析版) 题型:解答题
在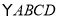 中,
中,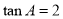 ,
,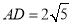 ,
, ,
,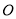 是
是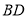 中点,
中点,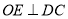 于
于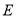 .
.

(1)求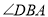 的度数.
的度数.
(2)求四边形 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省九年级上学期期末质量检测数学试卷(解析版) 题型:解答题
已知抛物线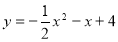 ,
,
(1)用配方法确定它的顶点坐标、对称轴;
(2) 取何值时,
取何值时, 随
随 增大而减小?
增大而减小?
(3) 取何值时,抛物线在
取何值时,抛物线在 轴上方?
轴上方?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com