
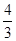 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
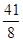 或5或
或5或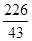
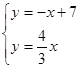 ,解得
,解得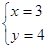 ,
,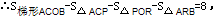
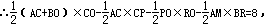
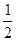 ×(7-t)×4=8,得t=3(舍)
×(7-t)×4=8,得t=3(舍)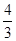 x中,得点Q的纵坐标为
x中,得点Q的纵坐标为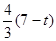
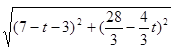

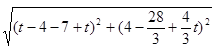
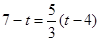 ,解得
,解得
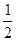 AP
AP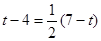 ,解得t=5.
,解得t=5.
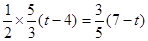 ,解得
,解得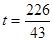
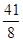 或5或
或5或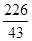 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
 与
与 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.
分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | 进价(元/台) | 售价(元/台) |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空 调 | 2400 | 2700 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com