
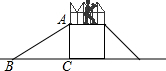
 如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度AC=2cm,滑梯着地点B与梯架之间的距离BC=4cm.
如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度AC=2cm,滑梯着地点B与梯架之间的距离BC=4cm.分析 (1)直接利用勾股定理得出AB的长,进而得出答案;
(2)直接利用特殊角的三角函数值,再结合tanB=$\frac{AC}{BC}$=$\frac{1}{2}$,得出答案.
解答 解:(1)由题意可得:在直角三角形ABC中,
AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$(cm),
答:滑梯AB的长为2$\sqrt{5}$cm;
(2)因为:tanB=$\frac{AC}{BC}$=$\frac{1}{2}$,tan45°=1,
所以0°<B<45°,故符合要求.
点评 此题主要考查了解直角三角形的应用以及坡角问题,正确把握坡角的定义是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
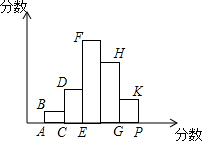 如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.
如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在锐角三角形ABC中,BC=5$\sqrt{2}$,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是5.
在锐角三角形ABC中,BC=5$\sqrt{2}$,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com