
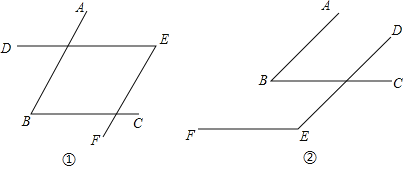
【题目】如图①②,![]() 的两边分别平行.
的两边分别平行.
(1)在图①中,![]() 与
与![]() 有什么数量关系?为什么?
有什么数量关系?为什么?
(2)在图②中,![]() 与
与![]() 有什么数量关系?为什么?
有什么数量关系?为什么?
(3)由(1)(2)你能得出什么结论?用一句话概括你得到的结论.
【答案】(1)∠B=∠E,理由见解析;(2)∠B+∠E=180°,理由见解析;(3)如果两个角的两边分别平行,那么这两个角相等或互补.
【解析】
(1)由已知AB∥EF,DE∥BC,根据平行线的性质得:∠B=∠EOC,∠EOC=∠E,即可得出答案;
(2)由已知AB∥DE,EF∥BC,得:∠B=∠DOC,∠BOE+∠E=180°,即可得出答案;(3)由(1)和(2)得出结论如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
解:(1)∠B=∠E
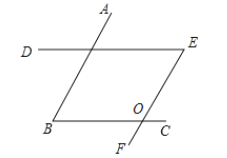
理由:∵BA∥EF,BC∥DE,
∴∠B=∠EOC,∠EOC=∠E,
∴∠B=∠E;
(2)∠B+∠E=180°

理由:∵BA∥ED,BC∥EF,
∴∠B=∠DOC,∠BOE+∠E=180°,
∵∠DOC=∠BOE,
∴∠B+∠E=180°;
(3)如果两个角的两边分别平行,那么这两个角相等或互补.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
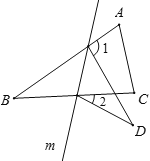
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
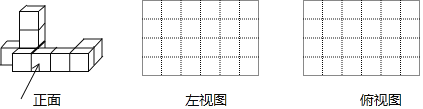
【题目】如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)正面图中有______块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影)
(3)用小正方体搭一个几何体,使得它的左视图和俯视图与你在(2)中所画的图一致,则这样的几何体最多要______块小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABD中,∠A=90°,AB=AD=2,作△ABD关于直线BD对称的△CBD,已知点F为线段AB上一点,且AF=m,连接CF,作∠FCE=90°,CE交AD的延长线于点E.
(1)求证:△BCF≌△DCE;
(2)若AE=n,且mn=3,求m2+n2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4 ![]() cm,则∠ACM的度数是( )
cm,则∠ACM的度数是( ) 
A.45°
B.50°
C.55°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com