(1)证明:如图(1),连接BE、BF.
∵AB是⊙O的直径,
∴∠AEB=90°.
又∵CD切⊙O于点B,
∴AB⊥BC,∠ABC=90°.
在Rt△AEB和Rt△ABC中,∠EAB=∠CAB,
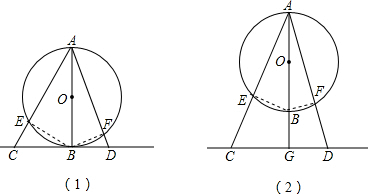
∴Rt△AEB∽Rt△ABC.
∴AE:AB=AB:AC,
即AE•AC=AB
2,
同理:Rt△AFB∽Rt△ABD,
∴AF:AB=AB:AD,
∴AF•AD=AB
2,
∴AE•AC=AF•AD.
(2)解:AE•AC=AF•AD仍然成立.
证明:如图(2),连接BE,BF,
∵直线l在向下平移时始终与AB垂直,垂足为G,则∠AGC=90°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠AGC=∠AEB,
又∵∠GAC=∠EAB,
∴Rt△AGC∽Rt△AEB,
∴AG:AE=AC:AB,
∴AE•AC=AG•AB,
同理:AF•AD=AG•AB,
∴AE•AC=AF•AD.
分析:(1)可通过构建相似三角形来求证.连接BE、BF,通过证Rt△AEB∽Rt△ABC与Rt△AFB∽Rt△ABD,得出AE、AC以及AF、AD和AB之间的关系,通过AB这个中间值来得出所求的比例关系.
(2)依然成立,因为这要能证得(1)中的两个三角形相似,就能得出(1)中的结论,直线l向下平移的过程中,两个三角形相似的条件(一个公共角,一组直角)没有改变,因此仍相似,所以(1)中的结论仍成立.
点评:此题考查了相似三角形的判定与性质以及切线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

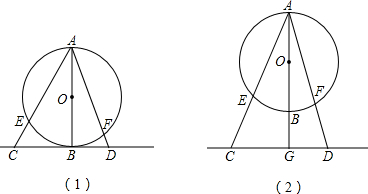
 ∴Rt△AEB∽Rt△ABC.
∴Rt△AEB∽Rt△ABC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

 如图,已知:AB是⊙O的直径,弦CD⊥AB于H,CE平分∠DCO交⊙O于点E.
如图,已知:AB是⊙O的直径,弦CD⊥AB于H,CE平分∠DCO交⊙O于点E.