
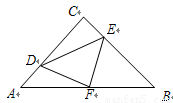
如图,在等腰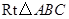 中,
中,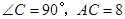 ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持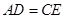 .连接DE、DF、EF.在此运动变化的过程中,下列结论:①
.连接DE、DF、EF.在此运动变化的过程中,下列结论:①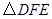 是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是【 】
是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是【 】
A.①②③ B.①③④ C.①④⑤ D.③④⑤
C
【解析】连接CF;
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF;
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形.
因此①正确.
当D、E分别为AC、BC中点时,四边形CDFE是正方形.
因此②错误.
∵△ADF≌△CEF,
∴S△CEF=S△ADF∴S四边形CEFD=S△AFC,
因此④正确.
由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;
即当DF⊥AC时,DE最小,此时DF=1/2 BC=4.
∴DE=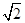 DF=4
DF=4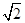 ;
;
因此③错误.
当△CEF面积最大时,由④知,此时△DEF的面积最小.
此时S△CEF=S四边形CEFD-S△DEF=S△AFC-S△DEF=16-8=8;
因此⑤正确.
故选C.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:2012-2013学年山东省文登市九年级下学期期中考试数学试卷(解析版) 题型:填空题
如图,在等腰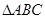 中,
中,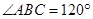 ,点
,点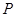 是底边
是底边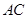 上一个动点,
上一个动点, 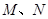 分别是
分别是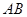 、
、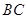 的中点.若
的中点.若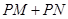 的最小值是2,则
的最小值是2,则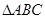 周长是 .
周长是 .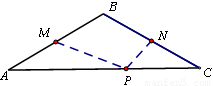
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川乐山沙湾区九年级毕业调研考试数学试卷(解析版) 题型:解答题
如图,在等腰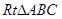 中,
中, ,
,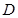 为斜边
为斜边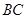 上的动点,若
上的动点,若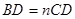 ,
,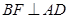 交
交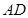 于
于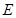 、
、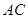 于
于 .
.
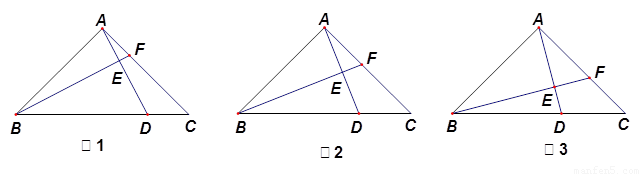
1.如图1,若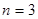 时,则
时,则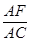 =
;
=
;
2.如图2,若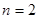 时,求证:
时,求证: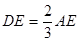
3.如图3,当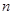 = 时,
= 时,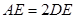 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com