
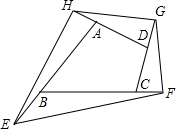
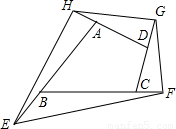
 如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为________(用含n的代数式表示).
如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为________(用含n的代数式表示).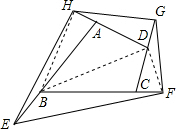 解:连接BH,BD,DF,
解:连接BH,BD,DF,

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
 11、如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为
11、如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为查看答案和解析>>
科目:初中数学 来源: 题型:
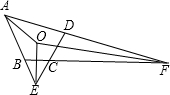 如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=
如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=查看答案和解析>>
科目:初中数学 来源: 题型:填空题
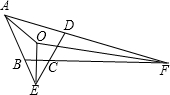
 如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=________.
如图,延长四边形ABCD对边AD,BC交于F;DC,AB交于E.如果∠AED,∠AFB平分线交于O,∠A=60°,∠BCD=130°,则∠EOF=________.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2008年12月浙江省宁波市余姚市世南中学九年级数学竞赛试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com