
| A.2 | B.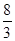 | C.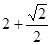 | D.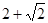 |
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
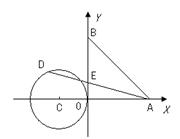
 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
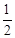 ;
;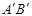 ,请写出线段
,请写出线段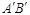 两个端点
两个端点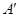 ,
,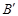 的坐标;
的坐标;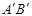 上对应点
上对应点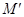 的坐标.
的坐标.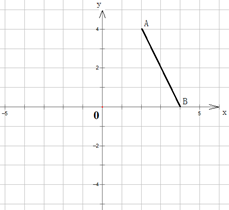
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
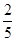 CD,GD=
CD,GD=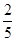 AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出tanα.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出tanα. 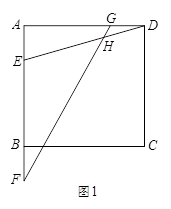
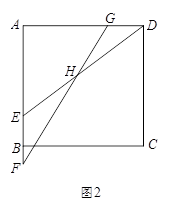
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com