
分析 (1)根据分式乘除法法则即可化简运算.
(2)根据因式分解以及分式的基本性质即可化简运算.
解答 解:(1)原式=$\frac{{a}^{2}}{{b}^{2}}•\frac{{b}^{2}}{{a}^{4}}$•$\frac{1}{4{a}^{2}{b}^{2}}$
=$\frac{1}{4{a}^{4}{b}^{2}}$
(2)原式=($\frac{{x}^{2}-2x-15}{x-5}$+$\frac{16}{x-5}$)•$\frac{5-x}{x-1}$
=-$\frac{{(x-1)}^{2}}{x-5}$•$\frac{x-5}{x-1}$
=1-x
点评 本题考查分式的混合运算,解题的关键是熟练运用因式分解以及分式的基本性质,本题属于基础题型.


科目:初中数学 来源: 题型:解答题
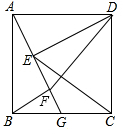 如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
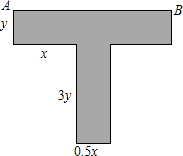 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com