
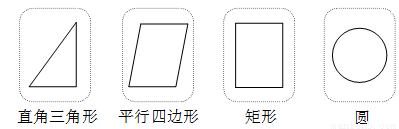
四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张卡片,则抽出的卡片上的图形是中心对称图形的概率为( )
A.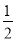 B.
B.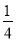 C.
C.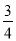 D.1
D.1
科目:初中数学 来源:2016届北京市通州区九年级4月一模数学试卷(解析版) 题型:选择题
下面四个图形分别是低碳、节水、节能和绿色食品标志,在这四个标志中,是轴对称图形的是( )

查看答案和解析>>
科目:初中数学 来源:2016届北京市顺义区九年级4月一模数学试卷(解析版) 题型:填空题
一张直角三角形纸片,其中有一个内角为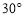 ,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是 .
,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是 .
查看答案和解析>>
科目:初中数学 来源:2016届北京市顺义区九年级4月一模数学试卷(解析版) 题型:选择题
如图,在已知的△ABC中,按以下步骤作图: ①分别以B,C为圆心,以大于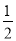 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )

A.90° B. 95° C.100° D. 105°
查看答案和解析>>
科目:初中数学 来源:2015-2016学年安徽省八年级下期中数学试卷(解析版) 题型:解答题
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代 数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你写出勾股定理内容(用文字语言表述):
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以(a+b)为高的直角梯形(如图2),请你利用图2,证明勾股定理.

查看答案和解析>>
科目:初中数学 来源:2015-2016学年安徽省八年级下期中数学试卷(解析版) 题型:填空题
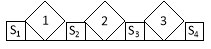
如图,依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放着的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= .
查看答案和解析>>
科目:初中数学 来源:2016届安徽省毕业班五校第四次联考数学试卷(解析版) 题型:解答题
某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com