Question

（1）如图1，已知正方形ABCD与正方形DEFG，点A、D、E三点共线，则S_△ADG______S_△DCE（填“＞”，“＜”或“=”）
（2）如图2，将图1中正方形DEFG绕点D，逆时针转到如图的位置，则S_△ADG______S_△DCE（填“＞”，“＜”或“=”）
请说明理由．
（3）如图3，以△ABC三边向外作三个正方形，分别为正方形AEDC、正方形CFGB正方形ABHK，并且△ABC的边AC长为5，边AB长为4，则三角形AKE，三角形CDF，三角形BGH的面积和的最大值为______．

Answer 1

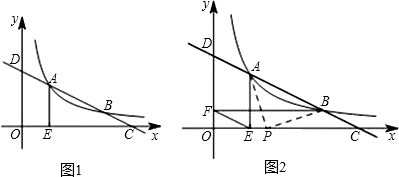
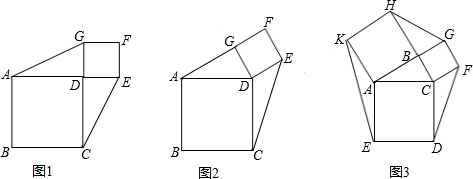
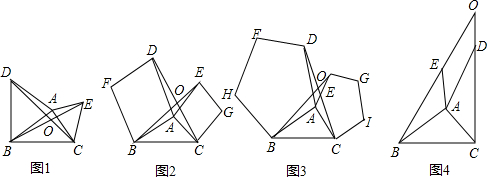
解：（1）∵正方形ABCD与正方形DEFG，点A、D、E三点共线，
∴AD=CD，DG=DE，
∵S_△ADG=AD×DG，S_△DCE=DE×CD，
∴S_△ADG=S_△DCE，
故答案为：=；

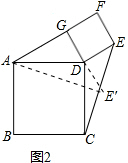
（2）把△DCE绕点D顺时针旋转90°，使CD与AD重合，E旋转到E'的位置，
∵四边形GDEF为正方形，∠GDE=90°，DG=DE=DE′，
∴G、D、E'在一直线上，且AD为△AGE'的中线，
∴S_△ADG=S_△ADE'=S_△CDE，
∴S_△ADG=S_△DCE，
故答案为：=；

（3）把△DCF绕点C顺时针旋转90°，使CD与AC重合，F旋转到F'的位置，
∵四边形BCFG为正方形，∠BCF=90°，BC=CF=CF′，
∴B、C、F'在一直线上，且AC为△ABF'的中线，
∴S_△CDF=S_△ACF'=S_△ABC，
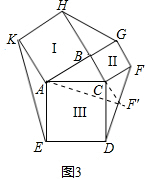
同理：S_△AEK=S_△HBG=S_△ABC，
所以△AKE，△CDF，△BGH的面积和为S_△ABC的3倍，
又AC长为5，边AB长为4，
∴S_{阴影部分面积}=3S_△ABC=3×AB×AC×sin∠ABC，
当∠ABC最大时△AKE，△CDF，△BGH的面积和最大，
即当AB⊥BC时，S_△ABC最大值为：×5×4=10
∴△AKE，△CDF，△BGH的面积和的最大值为10×3=30．
故答案为：30．
分析：（1）利用正方形ABCD与正方形DEFG，点A、D、E三点共线，得出AD=CD，DG=DE，进而得出S_△ADG=AD×DG，S_△DCE=DE×CD，即可得出答案；
（2）把△DCE绕点D顺时针旋转90°，使CD与AD重合，E旋转到E'的位置，得出四边形GDEF为正方形，∠GDE=90°，DG=DE=DE′，进而得出G、D、E'在一直线上，且AD为△AGE'的中线，得出S_△ADG=S_△ADE'=S_△CDE．
（3）把△DCF绕点C顺时针旋转90°，使CD与AC重合，F旋转到F'的位置，利用四边形BCFG为正方形，∠BCF=90°，BC=CF=CF′，得出B、C、F'在一直线上，且AC为△ABF'的中线，即可得出S_△CDF=S_△ACF'=S_△ABC，进而得出S_{阴影部分面积}=3S_△ABC=3×AB×AC×sin∠ABC，即可得出最值．
点评：本题考查了旋转的性质以及正方形的性质和三角形的面积公式，利用旋转性质得出旋转前后图形全等得出旋转图形是解题关键．