
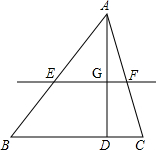
 EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.
EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.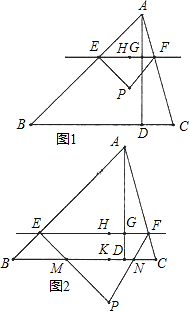 解:(1)∵EF∥BC,
解:(1)∵EF∥BC,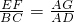 ,
,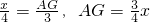 .
. ,
,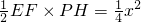 .
.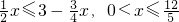 .
. ,
, ,
,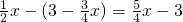 ,
,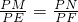 ,
, MN×PK=PK2=
MN×PK=PK2=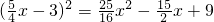 ,
,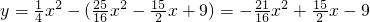 ,
,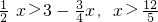
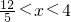 .
. x的关系;
x的关系; ,从而推出△PMN∽△PEF根据比例关系推出△PMN为等腰三角形,把△PMN用x表示出来,最后根据边长关系求出x的取值范围.
,从而推出△PMN∽△PEF根据比例关系推出△PMN为等腰三角形,把△PMN用x表示出来,最后根据边长关系求出x的取值范围.

科目:初中数学 来源: 题型:
 如图,△ABC的高CF、BG相交于点H,分别延长CF、BG与△ABC的外接圆交于D、E两点,则下列结论:①AD=AE;②AH=AE;③若DE为△ABC的外接圆的直径,则BC=AE.其中正确的是( )
如图,△ABC的高CF、BG相交于点H,分别延长CF、BG与△ABC的外接圆交于D、E两点,则下列结论:①AD=AE;②AH=AE;③若DE为△ABC的外接圆的直径,则BC=AE.其中正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC的高AD=4,BC=8,四边形MNPQ是△ABC中任意一个内接矩形
如图,△ABC的高AD=4,BC=8,四边形MNPQ是△ABC中任意一个内接矩形查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com