
 如下.
如下.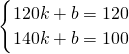



科目:初中数学 来源: 题型:
 如下.
如下.查看答案和解析>>
科目:初中数学 来源: 题型:
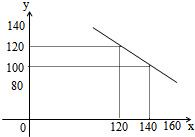
 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
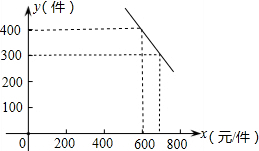
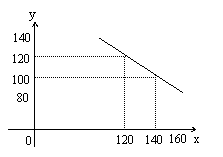
某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图。
(1)根据图象,求一次函数的解析式;
(2)当销售单价x在什么范围内取值时,销售量y不低于80件。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com