
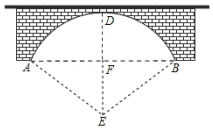
 如图,一圆弧形桥拱的圆心为E,拱桥的水面跨度AB=80米,桥拱到水面的最大高度DF为20米.求:
如图,一圆弧形桥拱的圆心为E,拱桥的水面跨度AB=80米,桥拱到水面的最大高度DF为20米.求:分析 (1)根据垂径定理和勾股定理求解;
(2)由垂径定理求出MH,由勾股定理求出EH,得出HF即可.
解答 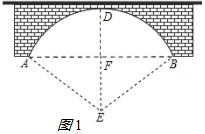 解:(1)如图,设点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
解:(1)如图,设点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB=$\frac{1}{2}$AB=40,EF=ED-FD=AE-DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
即桥拱的半径为50米;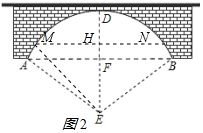
(2)设水面上涨后水面跨度MN为60米,MN交ED于H,连接EM,如图2所示
则MH=NH=$\frac{1}{2}$MN=30,
∴EH=$\sqrt{5{0}^{2}-3{0}^{2}}$=40(米),
∵EF=50-20=30(米),
∴HF=EH-EF=10(米);
故答案为:10.
点评 本题考查了垂径定理和勾股定理的运用;由垂径定理和勾股定理求出半径是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
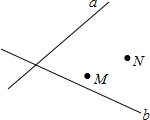 a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).
a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
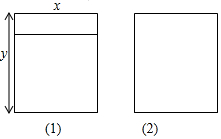 如图所示,是两种长方形铝合金窗框已知窗框的长都是y米,窗框宽都是x米,若一用户需(1)型的窗框2个,(2)型的窗框2个.
如图所示,是两种长方形铝合金窗框已知窗框的长都是y米,窗框宽都是x米,若一用户需(1)型的窗框2个,(2)型的窗框2个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com