
【题目】如图,在⊙O中,AB为直径,D.E为圆上两点,C为圆外一点,且∠E+∠C=90°.
(1)求证:BC为⊙O的切线.
(2)若sinA=![]() ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.

【答案】(1)证明见解析;(2)4.
【解析】试题分析:(1)根据在同圆或等圆中,同弧所对的圆周角相等可得∠A=∠E,再根据三角形的内角和等于180°求出∠ABC=90°,然后根据切线的定义证明即可;
(2)根据∠A的正弦求出AC,利用勾股定理列式计算求出AB,然后求解即可.
试题解析:(1)证明:∵∠A与∠E所对的弧都是![]() ,∴∠A=∠E,又∵∠E+∠C=90°,∴∠A+∠C=90°,在△ABC中,∠ABC=180°﹣90°=90°,∵AB为直径,∴BC为⊙O的切线;
,∴∠A=∠E,又∵∠E+∠C=90°,∴∠A+∠C=90°,在△ABC中,∠ABC=180°﹣90°=90°,∵AB为直径,∴BC为⊙O的切线;
(2)解:∵sinA=![]() ,BC=6,∴
,BC=6,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得AC=10,由勾股定理得,AB=
,解得AC=10,由勾股定理得,AB=![]() =
=![]() =8,∵AB为直径,∴⊙O的半径是
=8,∵AB为直径,∴⊙O的半径是![]() ×8=4.
×8=4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+4x﹣9=0时,原方程可变形为( )
A. (x+2)2=1 B. (x+2)2=7 C. (x+2)2=13 D. (x+2)2=19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在1000个数据中,用适当的方法抽取50个体为样本进行统计,频数分布表中54.5~57.5这一组的频率为0.12,估计总体数据落在54.5~57.5之间的约有( )个.
A.120B.60C.12D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE. 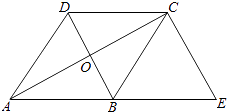
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如表所示(10分制).
甲 | 8 | 10 | 9 | 6 | 9 |
乙 | 10 | 8 | 9 | 7 | 8 |
(1)甲队成绩的中位数是分;
(2)乙队成绩的众数是分;
(3)分别计算甲队、乙队的方差;并判断哪队的成绩更稳定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近几年,某市持续大面积雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,调查结果共分为四个等组A.非常了解;B.比较了解;C.基本了解;D.不了解
根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾天气了解程度的 条形统计图 | 对雾霾天气了解程度的 扇形统计图 | 对雾霾天气了解程度的 统计表 | |
图1 |
图2 | 对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% | ||
B.比较了解 | m | ||
C.基本了解 | 45% | ||
D.不了解 | n | ||
请结合统计图表,回答下列问题:
(1)本次参与调查的学生选择“A.非常了解”的人数为__________人,m=__________,n=__________;
(2)请在图1中补全条形统计图;
(3)请计算在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遵义市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:

(1)参加调查测试的学生为多少人?
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在哪组内?
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com