
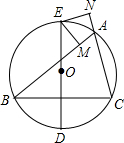
 如图,△ABC内接于⊙O,D是
如图,△ABC内接于⊙O,D是 的中点,DE为直径,EM⊥AB于M,EN⊥AC于N.
的中点,DE为直径,EM⊥AB于M,EN⊥AC于N.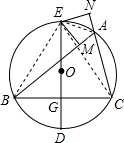 (1)证明:连BE、EC、AE,
(1)证明:连BE、EC、AE, 的中点,DE为直径,
的中点,DE为直径,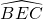 的中点,
的中点, =
= ,
, ,
, =
= ,
,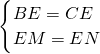 ,
,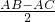 =
=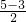 =1cm;
=1cm;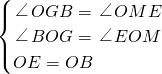 ,
, =
= .
. 的中点,DE为直径,可得出点E是
的中点,DE为直径,可得出点E是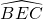 的中点,所以
的中点,所以 =
= ,再由四边形AEBC是圆内接四边形可得出∠EAN=∠CBE=∠BAE,根据AAS定理可知△AEM≌△AEN,故可得出结论;
,再由四边形AEBC是圆内接四边形可得出∠EAN=∠CBE=∠BAE,根据AAS定理可知△AEM≌△AEN,故可得出结论; =
= ,BE=CE,再由HL定力得出Rt△BME≌Rt△CNE,故BM=CN,即AB-AM=AB-AN=AC+AN,AN=
,BE=CE,再由HL定力得出Rt△BME≌Rt△CNE,故BM=CN,即AB-AM=AB-AN=AC+AN,AN=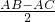 ,由此即可得出结论;
,由此即可得出结论; ,由此即可得出结论.
,由此即可得出结论.

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com