
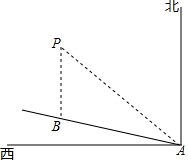
 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域,问这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域,问这艘船能否按原方向继续向前航行?为什么? 分析 过点B作BH⊥AP于H,过点P作PM⊥AB,交AB延长线于M.根据路程=速度×时间得出AB=24×$\frac{40}{60}$=16,根据方向角定义以及平行线性质得出∠BAP=75°-45°=30°.∠BPH=∠CAP=45°.解Rt△ABH,求出BH=$\frac{1}{2}$AB=8,AH=$\sqrt{3}$BH=8$\sqrt{3}$.解Rt△PBH,求出PH=BH=8,那么PA=PH+AH=8+8$\sqrt{3}$,PM=4+4$\sqrt{3}$>9,
即可判断这艘船能按原方向继续向前航行.
解答 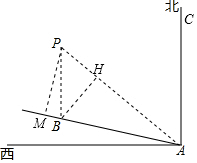 解:这艘船能按原方向继续向前航行.理由如下:
解:这艘船能按原方向继续向前航行.理由如下:
如图,过点B作BH⊥AP于H,过点P作PM⊥AB,交AB延长线于M.
由题意,知AB=24×$\frac{40}{60}$=16(海里),∠BAP=75°-45°=30°.
∵PB∥AC,
∴∠BPH=∠CAP=45°.
在Rt△ABH中,BH=$\frac{1}{2}$AB=8,AH=$\sqrt{3}$BH=8$\sqrt{3}$.
在Rt△PBH中,PH=BH=8,
∴PA=PH+AH=8+8$\sqrt{3}$,
∴PM=PA•sin∠PAM=$\frac{1}{2}$PA=4+4$\sqrt{3}$>9,
∴能按原方向继续向前航行.
点评 本题主要考查解直角三角形的应用-方向角问题,解答本题的关键是构造直角三角形,能利用三角函数表示相关线段的长度,难度一般.


科目:初中数学 来源: 题型:选择题
| A. | 一个游戏中奖的概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 为了了解一批炮弹的杀伤半径,应采用全面调查的方式 | |
| C. | 一组数据8,7,7,10,6,7,9的众数和中位数都是7 | |
| D. | 若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤6 | B. | a≥6 | C. | a<6 | D. | a≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com