
 ŇŃÖŞËıßĐÎABCDŁ¬µăEĘÇÉäĎßBCÉϵÄŇ»¸ö¶ŻµăŁ¨µăE˛»ÓëBˇ˘CÁ˝µăÖغϣ©Ł¬Ď߶ÎBEµÄ´ąÖ±Ć˝·ÖĎß˝»ÉäĎßACÓÚµăPŁ¬Á¬˝ÓDPŁ¬PEŁ®
ŇŃÖŞËıßĐÎABCDŁ¬µăEĘÇÉäĎßBCÉϵÄŇ»¸ö¶ŻµăŁ¨µăE˛»ÓëBˇ˘CÁ˝µăÖغϣ©Ł¬Ď߶ÎBEµÄ´ąÖ±Ć˝·ÖĎß˝»ÉäĎßACÓÚµăPŁ¬Á¬˝ÓDPŁ¬PEŁ® Ł¬ÉčAP=xŁ¬ˇ÷PCEµÄĂć»ýÎŞyŁ¬µ±APŁľ
Ł¬ÉčAP=xŁ¬ˇ÷PCEµÄĂć»ýÎŞyŁ¬µ±APŁľ ACʱŁ¬ÇóyÓëxÖ®ĽäµÄşŻĘýąŘϵʽŁ®
ACʱŁ¬ÇóyÓëxÖ®ĽäµÄşŻĘýąŘϵʽŁ®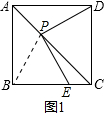 ˝âŁşŁ¨1Ł©PE=PDŁ¬PEˇÍPD
˝âŁşŁ¨1Ł©PE=PDŁ¬PEˇÍPD 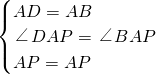 Ł¬
Ł¬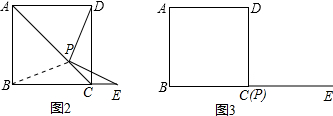
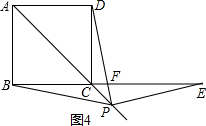
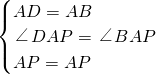 Ł¬
Ł¬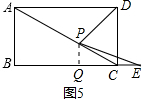
 =
= Ł¬
Ł¬ =
=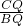 Ł¬
Ł¬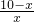 =
=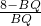 Ł¬
Ł¬ xŁ¬
xŁ¬ xŁ¬
xŁ¬ x-8Ł¬
x-8Ł¬ =
=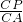 Ł¬
Ł¬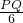 =
= Ł¬
Ł¬ xŁ¬
xŁ¬ ECˇÁPQŁ¬
ECˇÁPQŁ¬ Ł¨
Ł¨ x-8Ł©Ł¨ 6-
x-8Ł©Ł¨ 6- xŁ©Ł¬
xŁ©Ł¬ x2+
x2+ x-24Ł¨5ŁĽxŁĽ10Ł©Ł»
x-24Ł¨5ŁĽxŁĽ10Ł©Ł» =
= Ł¬
Ł¬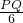 =
=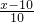 Ł¬
Ł¬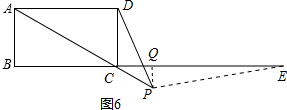
 x-6Ł¬
x-6Ł¬ =
=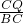 Ł¬
Ł¬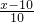 =
=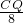 Ł¬
Ł¬ x-8Ł¬
x-8Ł¬ xŁ¬
xŁ¬ xŁ¬
xŁ¬ x-8Ł¬
x-8Ł¬ ECˇÁPQŁ¬
ECˇÁPQŁ¬ Ł¨
Ł¨ x-8Ł©Ł¨
x-8Ł©Ł¨ x-6Ł©Ł¬
x-6Ł©Ł¬ x2-
x2- x+24Ł¨xŁľ10Ł©Ł®
x+24Ł¨xŁľ10Ł©Ł®

 Č«ÓŵăÁ·µĄÔŞĽĆ»®ĎµÁĐ´đ°¸
Č«ÓŵăÁ·µĄÔŞĽĆ»®ĎµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐżÎłĚ | Ä꼶 | łőÖĐżÎłĚ |
| ¸ßŇ» | ¸ßŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ | łőŇ» | łőŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ß¶ţ | ¸ß¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ | łő¶ţ | łő¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ßČý | ¸ßČýĂâ·ŃżÎłĚÍĆĽöŁˇ | łőČý | łőČýĂâ·ŃżÎłĚÍĆĽöŁˇ |
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
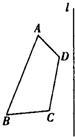 32ˇ˘ČçÍĽŁ¬ŇŃÖŞËıßĐÎABCDşÍÖ±ĎßLŁ®
32ˇ˘ČçÍĽŁ¬ŇŃÖŞËıßĐÎABCDşÍÖ±ĎßLŁ®˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
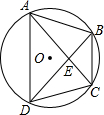 ČçÍĽŁ¬ŇŃÖŞËıßĐÎABCDĘǡŃOµÄÄÚ˝ÓËıßĐÎŁ¬ÇŇAB=CD=5Ł¬AC=7Ł¬BE=3Ł®ĎÂÁĐĂüĚâ´íÎóµÄĘÇŁ¨ˇˇˇˇŁ©
ČçÍĽŁ¬ŇŃÖŞËıßĐÎABCDĘǡŃOµÄÄÚ˝ÓËıßĐÎŁ¬ÇŇAB=CD=5Ł¬AC=7Ł¬BE=3Ł®ĎÂÁĐĂüĚâ´íÎóµÄĘÇŁ¨ˇˇˇˇŁ©| Aˇ˘ˇ÷ABEˇŐˇ÷DCE | Bˇ˘ˇĎBDA=45ˇă | Cˇ˘SËıßĐÎABCD=24.5 | Dˇ˘ÍĽÖĐČ«µČµÄČý˝ÇĐÎą˛ÓĐ2¶Ô |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş

˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş

Aˇ˘
| ||
Bˇ˘
| ||
Cˇ˘
| ||
Dˇ˘
|
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
˛éż´´đ°¸şÍ˝âÎö>>
ąúĽĘѧУÓĹѡ - Á·Ď°˛áÁбí - ĘÔĚâÁбí
şţ±±Ęˇ»ĄÁŞÍřÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨Ć˝Ě¨ | ÍřÉĎÓĐş¦ĐĹϢľŮ±¨×¨Çř | µçĐĹթƾٱ¨×¨Çř | ÉćŔúĘ·ĐéÎŢÖ÷ŇĺÓĐş¦ĐĹϢľŮ±¨×¨Çř | ÉćĆóÇÖȨľŮ±¨×¨Çř
ÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨µç»°Łş027-86699610 ľŮ±¨ÓĘĎ䣺58377363@163.com