
分析 (1)根据已知条件得到p2=$\frac{a-1}{a}$,p3=$\frac{-1}{a-1}$,p4=a,于是得到结论;
(2)根据(1)中的规律即可得到结果.
解答 解:(1)∵p1=a,
∴p2=1-$\frac{1}{{p}_{1}}$=1-$\frac{1}{a}$=$\frac{a-1}{a}$,
∴p3=1-$\frac{a}{a-1}$=$\frac{-1}{a-1}$,
∴p4=1+(a-1)=a,
故答案为:$\frac{-1}{a-1}$,a;
(2)2018÷3=672…2,
∴p2018=$\frac{a-1}{a}$,
故答案为:$\frac{a-1}{a}$.
点评 本题考查了规律型:数字的变化类,找准规律是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
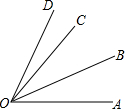 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )| A. | 70° | B. | 83° | C. | 68° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
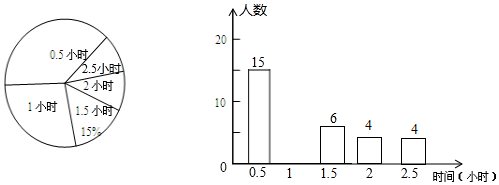
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C. | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:| 平均数 | 中位数 | 众数 | 方差 | |
| 八(一)班 | 8.5 | 8.5 | 8.5 | 0.7 |
| 八(二)班 | 8.5 | 8 | 10 | 1.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com