
阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:湖南省邵阳市2018届九年级中考数学模拟试卷(5) 题型:单选题
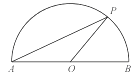
如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是
A. 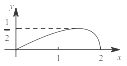 B.
B. 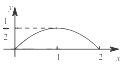 C.
C.  D.
D. 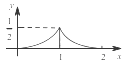
查看答案和解析>>
科目:初中数学 来源:2018秋人教版九年级数学上册:第二十一章一元二次方程章末检测题(B) 题型:单选题
有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )
A. 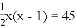 B.
B. 
C. 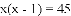
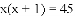
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市2017-2018学年九年级6月中考数学模拟试卷 题型:填空题
袋子中装有红、黄、绿三种颜色的小球各一个,从中任意摸出一个放回搅匀,再摸出一个球,则两次摸出的球都是黄色的概率是_____.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市2017-2018学年九年级6月中考数学模拟试卷 题型:单选题
下列事件中,属于必然事件的是( )
A. 随时打开电视机,正在播新闻
B. 优秀射击运动员射击一次,命中靶心
C. 抛掷一枚质地均匀的骰子,出现4点朝上
D. 长度分别是3cm,5cm,6cm的三根木条首尾相接,组成一个三角形
查看答案和解析>>
科目:初中数学 来源:2018年河南省南阳市镇平县中考数学模拟试卷 题型:解答题
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本为________,样本容量为_______;
(2)在频数分布表中,a=______,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?

查看答案和解析>>
科目:初中数学 来源:2018年河南省南阳市镇平县中考数学模拟试卷 题型:单选题
有一组数据x1,x2,…xn的平均数是2,方差是1,则3x1+2,3x2+2,…+3xn+2的平均数和方差分别是( )
A. 2,1 B. 8,1 C. 8,5 D. 8,9
查看答案和解析>>
科目:初中数学 来源:2018年江苏省苏州市太仓市中考数学模拟试卷(6月份) 题型:填空题
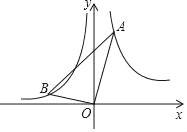
如图,点A是反比例函数y= (x>0)图象上的一点,点B是反比例函数y=﹣
(x>0)图象上的一点,点B是反比例函数y=﹣ (x<0)图象上的点,连接OA、OB、AB,若∠AOB=90°,则sin∠A=_____
(x<0)图象上的点,连接OA、OB、AB,若∠AOB=90°,则sin∠A=_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com