
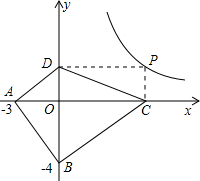
 (1)探索归纳.用等号或不等号填空:
(1)探索归纳.用等号或不等号填空: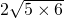
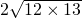
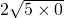
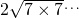
 上任意一点,过点P作PC⊥x轴于C,过点p作PD⊥y轴于D,连接AB、BC、CD、DA.
上任意一点,过点P作PC⊥x轴于C,过点p作PD⊥y轴于D,连接AB、BC、CD、DA.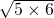 =
=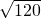 ,120<121,
,120<121,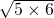 ;
;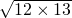 =
= <
<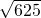 =25,
=25,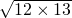 ;
;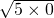 =0,
=0,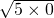 ;
;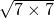 =14,
=14,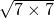 .
. .
. -
- )2≥0,
)2≥0, +b≥0,
+b≥0, ,只有点a=b时,等号成立.
,只有点a=b时,等号成立. ),则C(x,0),D(0,
),则C(x,0),D(0, ),CA=x+3,DB=+4,
),CA=x+3,DB=+4, CA×DB=
CA×DB= (x+3)×(
(x+3)×( +4),
+4), )+12,
)+12, >0,
>0, ≥2
≥2 =6,
=6, ,即x=3时,等号成立.
,即x=3时,等号成立.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:

| 序号 | ① | ② | ③ | ④ | … |
| S | 2 | 2.5 | 3 | 4 | … |
| x | 4 | 5 | 6 | 8 | … |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com