
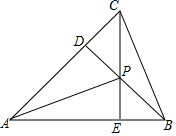
 如图,△ABC的两条高BD、CE相交于点P,且PD=PE.求证:AC=AB.
如图,△ABC的两条高BD、CE相交于点P,且PD=PE.求证:AC=AB. 分析 易证∠CAP=∠BAP,再证明∠DCP=∠EBP即可证明△APC≌△APB,由全等三角形的性质即可得到AC=AB.
解答 证明:
∵BD,CE是△ABC的两条高,
∴CE⊥AB,BD⊥AC,
又∵PD=PE,
∴点P在∠BAC的角平分线上,
∴∠CAP=∠BAP,
∵∠DPC=∠EPC,∠CDP=∠BEP=90°,
∴∠DCP=∠EBP,
在△APC和△APB中
$\left\{\begin{array}{l}{∠ACP=∠ABP}\\{∠CAP=∠BAP}\\{AP=AP}\end{array}\right.$,
∴△APC≌△APB(AAS),
∴AC=AB.
点评 本题考查了全等三角形的判断和性质以及角平分线性质逆定理的运用,熟记全等三角形的各种判断方法是证题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD=CD,AB=BC,AC与BD交于点O.我们把这种两组邻边分别相等的四边形叫做“筝形”.请你猜想筝形的两条对角线AC与BD之间的位置关系,并证明你的结论.
如图,四边形ABCD中,AD=CD,AB=BC,AC与BD交于点O.我们把这种两组邻边分别相等的四边形叫做“筝形”.请你猜想筝形的两条对角线AC与BD之间的位置关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
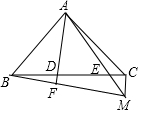 已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.
已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
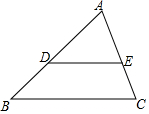 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=12,AE=6,EC=4.则AD=$\frac{36}{5}$.
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=12,AE=6,EC=4.则AD=$\frac{36}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
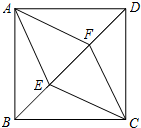 如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF、AE、CE、CF,请你判断四边形AECF的形状,并证明你的结论.
如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF、AE、CE、CF,请你判断四边形AECF的形状,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com