

分析 (1)根据1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按顺序排列,可得每四个数一循环,根据第几排就有几个数,可得前n排数的个数为(1+2+3+…+n)=$\frac{(1+n)n}{2}$,根据前四排的总数加上第五排的四个数,可得第五排的第四个数,根据前十四排的总数加上第五排的7个数,可得第十五排的第七个数,根据实数的乘法,可得答案;
(2)根据前90排的总数加第100排的个数10,可得答案.
解答 解:(1)(5,4)表示$\sqrt{2}$,
第一排一个数,第二排两个数,第三排三个数,第n排n个数,
前n排数的个数为(1+2+3+…+n)=$\frac{(1+n)n}{2}$,
前十四排的数的个数加7:(1+2+3+4+…+13+14)+7=$\frac{(1+14)×14}{2}$+7=112,
第112个数是112÷4=38,即(15,7)表示$\sqrt{6}$,
表示(5,4)与(15,7)表示的两数之积$\sqrt{2}$×$\sqrt{6}$=2$\sqrt{3}$;
(2)前99排的数加10:(1+2+3+4++…89+99)+10=$\frac{(1+99)×99}{2}$+10=4960,
4960÷4=1240,即1240轮的最后一个数1,
即(100,10)表示的数是$\sqrt{6}$.
点评 本题考查了算术平方根,利用排列顺序得出每四个数一循环,第几排有几个数是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
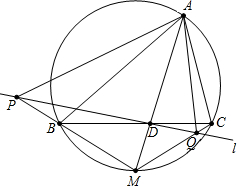 如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )
如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )| A. | 无论直线l的位置如何,总有直线PM与△ABD的外接圆相切 | |
| B. | 无论直线l的位置如何,总有∠PAQ>∠BAC | |
| C. | 直线l选取适当的位置,可使A、P、M、Q四点共圆 | |
| D. | 直线l选取适当的位置,可使S△APQ<S△ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com