Question

8．如图，在平面直角坐标系中存在矩形ABCO，点A（a，0）、点B（a，b），且a、b满足：$\sqrt{a-4}$+（b-m）²=0（实数m＞4）．
（1）求A点坐标；
（2）作∠OAB的角平分线交y轴于D，AD的中点为E，作EF⊥BE交x轴于F，求$\frac{AF}{OF}$的值（用m表示）；
（3）在（2）的条件下，当m=12时，将矩形ABCO向右推得到矩形A'B'C'O'，使A与A'重合，B'落在x轴上．现在将矩形沿射线AD以1个单位/秒平移，设平移时间为t，用t表示平移过程中矩形ABCD与矩形A'B'C'O'重合部分的面积．

Answer 1

分析 （1）利用非负数的性质求出a、b即可解决问题；
（2）如图1中，连接OE，只要证明△OEF≌△AEB（ASA），可得OF=AB=m，由此即可解决问题；
（3）分三种情形讨论求解①如图2中，当0≤t≤4$\sqrt{2}$时，重叠部分是四边形MNA′O′．②如图3中，当4$\sqrt{2}$＜t≤8$\sqrt{2}$时，重叠部分是四边形MNKP．③如图4中，当8$\sqrt{2}$＜t≤12$\sqrt{2}$时，重叠部分是四边形BMPC．④当t＞12$\sqrt{2}$t时，没有重叠部分；

解答 解：（1）∵$\sqrt{a-4}$+（b-m）²=0，
又∵$\sqrt{a-4}$≥0，（b-m）²≥0，
∴$\sqrt{a-4}$=0，（b-m）²=0，
∴a=4，b=m，
∴A（4，0）．

（2）如图1中，连接OE，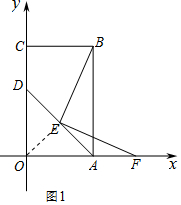

在矩形ABCO中，∠OAB=90°，
∵AD平分∠OAB，
∴∠OAD=∠BAD=45°，
在Rt△AOD中，AD的中点为E
∴OE=AE，
∴∠EOA=∠EAO=∠EAB=45°，
∴∠OEA=90°，
又∵EF⊥BE，即∠BEF=90°，
∴∠OEF=∠AEB，
∴△OEF≌△AEB（ASA），
∴OF=AB=m，
∴$\frac{AF}{OF}$=$\frac{OF-OA}{OF}$=$\frac{m-4}{m}$．

（3）①如图2中，当0≤t≤4$\sqrt{2}$时，重叠部分是四边形MNA′O′，
S=MN•NA′=4×$\frac{\sqrt{2}}{2}$t=2$\sqrt{2}$t．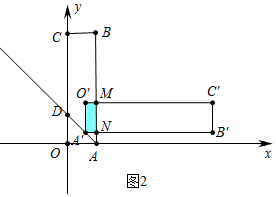

②如图3中，当4$\sqrt{2}$＜t≤8$\sqrt{2}$时，重叠部分是四边形MNKP，
S=16．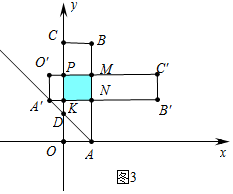


③如图4中，当8$\sqrt{2}$＜t≤12$\sqrt{2}$时，重叠部分是四边形BMPC，
S=48-4×$\frac{\sqrt{2}}{2}$t=48-2$\sqrt{2}$t．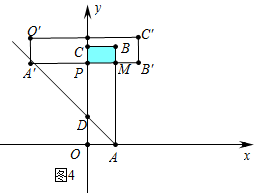


④当t＞12$\sqrt{2}$t时，S=0．

点评 本题考查矩形的性质、全等三角形的判定和性质、对边相等面积等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形，属于中考压轴题．