
����Ŀ�����Ķ����ϣ�
���ڶ�������ʽ![]() ����ֱ�ӷֽ�Ϊ
����ֱ�ӷֽ�Ϊ![]() ����ʽ�������ڶ�������ʽ
����ʽ�������ڶ�������ʽ![]() ���Ͳ���ֱ���ù�ʽ�ˣ����ǿ����ڶ�������ʽ
���Ͳ���ֱ���ù�ʽ�ˣ����ǿ����ڶ�������ʽ![]() ���ȼ���һ��
���ȼ���һ��![]() ��ʹ���Ϊ��ȫƽ��ʽ���ټ�ȥ
��ʹ���Ϊ��ȫƽ��ʽ���ټ�ȥ![]() ���(����Ҳ�ɰ�
���(����Ҳ�ɰ�![]() ���
���![]() ��
��![]() �ĺ�)��ʹ����ʽ�ӵ�ֵ���䣮
�ĺ�)��ʹ����ʽ�ӵ�ֵ���䣮
������![]()
![]()
![]()
![]()
![]()
![]() ��
��
���ǰ�����������������ʽ�ֽ���ʽ�ķ���������(��)���
��Ӧ�ò��ϣ�
![]() ��ʽ����(��)����Ȱ���ȫƽ��ʽ�����һ��Ȼ����______��ʵ�ַֽ���ʽ��
��ʽ����(��)����Ȱ���ȫƽ��ʽ�����һ��Ȼ����______��ʵ�ַֽ���ʽ��
![]() ������ݲ������ṩ����ʽ�ֽ�ķ�����������Ķ���ʽ�ֽ���ʽ��
������ݲ������ṩ����ʽ�ֽ�ķ�����������Ķ���ʽ�ֽ���ʽ��
![]() ��
��
![]()
 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
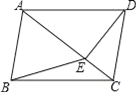
����Ŀ����ͼ�����ı���ABCD�У�AB��CD����ABC=��ADC��DE��ֱ�ڶԽ���AC��������E������BE��
��1����֤���ı���ABCD��ƽ���ı��Σ�
��2����AB=BE=2��sin��ACD=![]() �����ı���ABCD�������
�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ������ѧ���̳�����ס������ֲ�ͬ���������������3000Ԫ����������������2100Ԫ������������������ǹ�����������������2�����ҹ���һ����������ȹ���һ����������20Ԫ��
��1������һ����������һ����������������Ԫ��
��2��Ϊ��Ӧ�����������У���ĺ��٣�����ѧУ�����ٴι���ס�����������50����ǡ����̳�������������ۼ۽��е��������������ۼ۱ȵ�һ�ι���ʱ�����10%�����������ۼ۱ȵ�һ�ι���ʱ������10%������˴ι���ס�������������ܷ��ò�����2950Ԫ����ô����ѧУ���ɹ�����ٸ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡ�����У�Ϊ�˽�ijУѧ���Ŀ�����Ȥ���������ij����С����������Ķ������������������鷨�������������ĸ�ѡ�����������ķ��������˸�У����ѧ���Ŀ�����Ȥ���������ÿ��ѧ������ѡһ����ֻ��ѡһ��������ݵ���������������ͳ��ͼ��
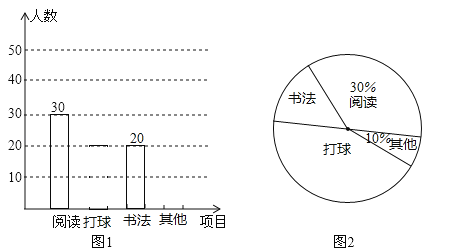
����ͳ��ͼ���ṩ����Ϣ������������⣺
��1�����γ��������е����������� ��
��2����ȫ����ͳ��ͼ��
��3����У����2000��ѧ���������ͳ�ƽ�����Ƹ�У������Ȥ����Ϊ����������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
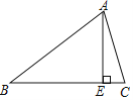
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ĸߣ�
�ĸߣ�
![]() ����
����![]() �Ľ�ƽ����
�Ľ�ƽ����![]() �������
�������![]() �Ķ�����
�Ķ�����
![]() ֱ��д��
ֱ��д��![]() ��
��![]() ��
��![]() ����֮���������ϵ��
����֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��������5�����ۣ���abc��0����b��a��c����4a+2b+c��0����2c��3b����a+b��m��am+b������m��1��ʵ������2a+b+c��0��������ȷ�Ľ��۵��У�������
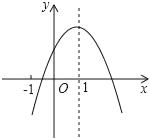
A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
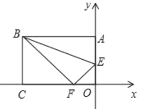
����Ŀ��������ֽƬ![]() �У�
��![]() ��
��![]() �������ų�����ֽƬ
�������ų�����ֽƬ![]() ��ͼ������ƽ��ֱ������ϵ�У��ڱ�
��ͼ������ƽ��ֱ������ϵ�У��ڱ�![]() ��ȡһ��
��ȡһ��![]() ����
����![]() ��
��![]() �۵���ʹ��
�۵���ʹ��![]() ǡ������
ǡ������![]() ���ϵĵ�
���ϵĵ�![]() ����
����
��1����![]() ��������____________________����
��������____________________����![]() ��������__________________________��
��������__________________________��
��2����![]() ����һ��
����һ��![]() ��ʹ
��ʹ![]() ��С�����
��С�����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£���![]() ��ֱ��
��ֱ��![]() ��һ�����㣬��
��һ�����㣬��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ��� ��ϵʽ��
�ĺ��� ��ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ź�˾�ֻ���ͨѶ����![]() ��
��![]() ����ҵ�����ͣ�
����ҵ�����ͣ�![]() ��շѱ��ǣ�����ͨ��ʱ����ÿ���ֻ�ÿ�±���������12Ԫ�����⣬ͨ���Ѱ�0��2Ԫ/���Ӽƣ�
��շѱ��ǣ�����ͨ��ʱ����ÿ���ֻ�ÿ�±���������12Ԫ�����⣬ͨ���Ѱ�0��2Ԫ/���Ӽƣ�![]() ��շѱ��ǣ�û�����⣬��ͨ���Ѱ�0��25Ԫ/���Ӽƣ���ͼ��ʾ����ÿ��Ӧ�ɷ���
��շѱ��ǣ�û�����⣬��ͨ���Ѱ�0��25Ԫ/���Ӽƣ���ͼ��ʾ����ÿ��Ӧ�ɷ���![]() ��Ԫ����ͨ��ʱ��
��Ԫ����ͨ��ʱ��![]() �����ӣ�֮��ĺ���ͼ�����н��ۣ�
�����ӣ�֮��ĺ���ͼ�����н��ۣ�
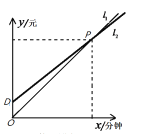
��ͼ��![]() ��
��![]() ����շѷ�ʽ����ʾ�ĺ���ͼ��
����շѷ�ʽ����ʾ�ĺ���ͼ��
��������µ�ͨ��ʱ��Ϊ180���ӣ�����ѡ��![]() �ʡǮ��
�ʡǮ��
���������Ԥ����100Ԫ�Ļ��ѣ�����ѡ��![]() ����㣻
����㣻
����![]() ���
���![]() ��Ļ��Ѷ�10Ԫ����
��Ļ��Ѷ�10Ԫ����![]() ���
���![]() ���ͨ��ʱ�䶼��40���ӻ�
���ͨ��ʱ�䶼��40���ӻ�![]() ���
���![]() ���ͨ��ʱ���40������
���ͨ��ʱ���40������![]() ���
���![]() ���ͨ��ʱ��ֱ�Ϊ240���Ӻ�200���ӣ�������ȷ�Ľ����У� ��
���ͨ��ʱ��ֱ�Ϊ240���Ӻ�200���ӣ�������ȷ�Ľ����У� ��
A.�٢ڢۢ�B.�ڢۢ�C.�ڢ�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
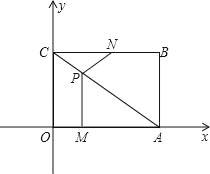
����Ŀ����ͼ��ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ���A��B������ֱ�Ϊ��4��0������4��3��������M��N�ֱ��O��Bͬʱ��������ÿ��1����λ���ٶ��˶������У���M��OA���յ�A�˶�����N��BC���յ�C�˶�������M��MP��OA����AC��P������NP����֪�����˶���x�룮
��1����P������꣨�ú�x�Ĵ���ʽ��ʾ����
��2��������NPC���S�ı���ʽ����������S�����ֵ����Ӧ��xֵ��
��3�����ı���OMPC�����ΪS1���ı���ABNP�����ΪS2�������x��ȡֵ��Χ����S1��S2�Ĵ�С��ϵ��˵�����ɣ�
��4����xΪ��ֵʱ����NPC��һ�����������Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com