
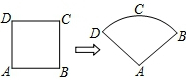
 如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度.(结果保留π)
如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度.(结果保留π) 科目:初中数学 来源: 题型:填空题
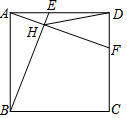 如图,正方形ABCD的边AD、CD上两个动点E,F,且满足AF=BE,BE交AF于点H.若正方形的边长为4,线段DH最大值为x,最小值为y,则$\sqrt{x}$-y的值是4-2$\sqrt{5}$.
如图,正方形ABCD的边AD、CD上两个动点E,F,且满足AF=BE,BE交AF于点H.若正方形的边长为4,线段DH最大值为x,最小值为y,则$\sqrt{x}$-y的值是4-2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
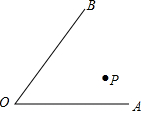 如图,∠AOB内有一点P
如图,∠AOB内有一点P查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
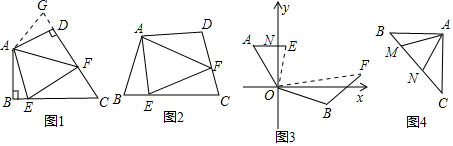
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
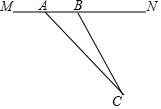 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
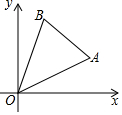 如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)
如图,在平面直角坐标系中,点A(a,b),B(c,a)均在第一象限,且c=$\sqrt{5a}$•$\sqrt{\frac{4a}{5}}$-$\sqrt{9{b}^{2}}$(b<a<3b)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com