
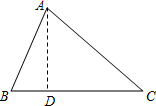
 如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?
如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?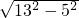 =12,
=12, BC•AD=
BC•AD= ×14×12=84(平方米),
×14×12=84(平方米),

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
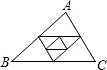 如图,△ABC的三条中位线组成一个新三角形,这个新三角形的三条中位线又组成一个小三角形,则这个小三角形的周长是原△ABC周长的( )
如图,△ABC的三条中位线组成一个新三角形,这个新三角形的三条中位线又组成一个小三角形,则这个小三角形的周长是原△ABC周长的( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
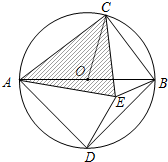 若在⊙O内存在点E,使AE=AD,CB=CE.
若在⊙O内存在点E,使AE=AD,CB=CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 在如图中,每个小正方形的边长都是1,先把△ABC向右平移6个小方格,再绕点A的对应点逆时针方向旋转90度得到一个新的三角形.画出平移和旋转后的图形,标明对应字母.
在如图中,每个小正方形的边长都是1,先把△ABC向右平移6个小方格,再绕点A的对应点逆时针方向旋转90度得到一个新的三角形.画出平移和旋转后的图形,标明对应字母.查看答案和解析>>
科目:初中数学 来源: 题型:
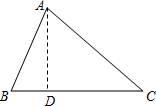 如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?
如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com