
【题目】设![]() ,
, ![]() ,……,
,……, ![]() ,(n为正整数)
,(n为正整数)
(1)试说明![]() 是8的倍数;
是8的倍数;
(2)若△ABC的三条边长分别为![]() 、
、![]() 、
、![]() (
(![]() 为正整数)
为正整数)
①求![]() 的取值范围.
的取值范围.
②是否存在这样的![]() ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
【答案】(1)证明见解析(2)①k>1;②当k=5时,△ABC的周长为一个完全平方数.
【解析】试题分析:(1)根据题意可以对an进行化简,从而可以解答本题;(2)①根据(1)中的结果,可以得到ak、ak+1、ak+2的值,从而可以得到k的取值范围;②根据①中ak、ak+1、ak+2的值,可以求得△ABC的周长,从而可以解答本题.
试题解析:(1)∵an=(2n+1)2﹣(2n﹣1)2
=[(2n+1)﹣(2n﹣1)][(2n+1)+(2n﹣1)]=2×4n=8n,
∵8n能被8整除,∴an是8的倍数;
(2)①由(1)可得,ak=8k,ak+1=8(k+1),ak+2=8(k+2),
∴8k+8(k+1)>8(k+2),解得,k>1,即k的取值范围是:k>1;
②存在这样的k,使得△ABC的周长为一个完全平方数,
理由:∵△ABC的周长是:8k+8(k+1)+8(k+2)=24k+24=24(k+1)=4×6×(k+1),
∴△ABC的周长为一个完全平方数,则k+1=6得k=5即可,
即当k=5时,△ABC的周长为一个完全平方数.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,点A(a,b)是双曲线y=![]() (x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.
(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于点C,过点A作AD⊥x轴于点D,连接AP交y轴于点B.

(1)△PAC的面积是 ;
(2)当a=2,点P的坐标为(﹣2,0)时,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知28a2bm÷4anb2=7b2,那么m,n的值为( )
A. m=4,n=2 B. m=4,n=1 C. m=1,n=2 D. m=2,n=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. (3)+(4)= 3+4= 7 B. (3)+(4)= 3+4= 7
C. (3)(4)=3+4= 1 D. (3)(4)=34=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
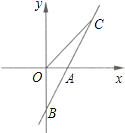
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com