
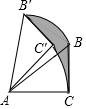
 如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.
如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$. 分析 根据题意和图形可以得到阴影部分的面积是扇形ABB′的面积与△ABC的面积之和减去△AB′C′的面积再减去扇形ACC′的面积,从而可以解答本题.
解答 解:∵在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,
∴△ABC≌△AB′C′,
∴线段BC扫过的区域(图中阴影部分)面积为:S扇形ABB′+S△ABC-S△AB′C′-S扇形ACC′=S扇形ABB′-S扇形ACC′=$\frac{45×π×A{B}^{2}}{360}-\frac{45×π×A{C}^{2}}{360}$=$\frac{π(A{B}^{2}-A{C}^{2})}{8}=\frac{π•B{C}^{2}}{8}=\frac{25π}{8}$,
故答案为:$\frac{25π}{8}$.
点评 本题考查扇形面积的计算、旋转的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{35}{2}$ | B. | 10 | C. | 8$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
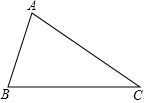 如图,已知△ABC,按要求画图、填空:
如图,已知△ABC,按要求画图、填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com