(1)证明:延长AD、EF交于点G,

当k=1时,DE=BD
∵EF∥AB,∴∠BAD=∠EGD,
又∵∠BDA=∠EDG,BD=ED,
∴△ABD≌△GED,
∴AB=GE,
又∵AD平分∠BAC,
∴∠BAD=∠DAC,
∴∠FGD=∠DAC,
∴AF=GF,
∴AF+EF=AB
(2)解:根据(1)可得线段AF、EF、AB之间满足数量关系:AF+EF=2AB;
(3)解:延长AD、EF交点为G.
由(1)(2)可知:FG+EF=2AB=18,即GE=18.
过点A作AH⊥GE,在Rt△AGH中,tan∠G=tan∠DAF=

.
即

∴GH=2AH
设AH=x,则GH=2x,HE=18-2x,
在Rt△AEH中,由勾股定理可得x
2+

,解得

,
当AH=8时,GH=16,设FH=a,则AF=16-a,在Rt△AFH中,
由勾股定理可得:8
2+a
2=(16-a)
2,
解得a=6,AF=10,EF=8,成立.
当AH=

时,同理可求FH=4.8,AF=8,EF=10.

∵AF>EF,∴此种情况不成立.
∵EF∥AB,∴∠ABC=∠FEC,又∵∠ACB=∠FCE.
∴△ABC∽△FEC,
∴

即

∴AC=

.
分析:(1)延长AD、EF交于点G,当k=1时,DE=BD,再根据∠BDA=∠EDG,BD=ED,证出△ABD≌△GED,得出AB=GE,又因为∠BAD=∠DAC,所以∠FGD=∠DAC,AF=GF,
即可证出AF+EF=AB;
(2)当k=2时,根据(1)即可直接写出线段AF、EF、AB之间满足得数量关系;
(3)延长AD、EF交点为G,由(1)(2)可知GE=18,过点A作AH⊥GE,在Rt△AGH中,

,所以GH=2AH,设AH=x,则GH=2x,HE=18-2x,在Rt△AEH中,由勾股定理可得x
2+

,解得

,当AH=8时,在Rt△AFH中,8
2+a
2=(16-a)
2,解得a=6,AF=10,EF=8,成立,当AH=

时,因为AF>EF,此种情况不成立,因为EF∥AB,所以∠ABC=∠FEC,又因为∠ACB=∠FCE,可以得出△ABC∽△FEC,所以

即

,即可求出AC的值.
点评:此题考查了相似三角形的判定和性质,关键是根据相似三角形的性质列出方程,要注意的是(3)中,要进行分类求解.

 =k,过E作EF∥AB交AC的延长线于F.
=k,过E作EF∥AB交AC的延长线于F. ,AE=2
,AE=2 ,且AF>EF,求边AC的长.
,且AF>EF,求边AC的长.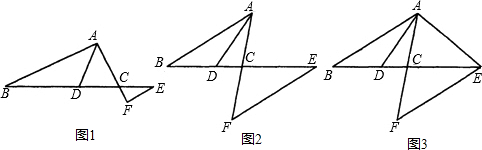

 .
. ∴GH=2AH
∴GH=2AH ,解得
,解得 ,
, 时,同理可求FH=4.8,AF=8,EF=10.
时,同理可求FH=4.8,AF=8,EF=10.
 即
即
 .
. ,所以GH=2AH,设AH=x,则GH=2x,HE=18-2x,在Rt△AEH中,由勾股定理可得x2+
,所以GH=2AH,设AH=x,则GH=2x,HE=18-2x,在Rt△AEH中,由勾股定理可得x2+ ,解得
,解得 ,当AH=8时,在Rt△AFH中,82+a2=(16-a)2,解得a=6,AF=10,EF=8,成立,当AH=
,当AH=8时,在Rt△AFH中,82+a2=(16-a)2,解得a=6,AF=10,EF=8,成立,当AH= 时,因为AF>EF,此种情况不成立,因为EF∥AB,所以∠ABC=∠FEC,又因为∠ACB=∠FCE,可以得出△ABC∽△FEC,所以
时,因为AF>EF,此种情况不成立,因为EF∥AB,所以∠ABC=∠FEC,又因为∠ACB=∠FCE,可以得出△ABC∽△FEC,所以 即
即 ,即可求出AC的值.
,即可求出AC的值.

 名题金卷系列答案
名题金卷系列答案