Question

6．如图，A是以BC为直径的⊙O上一点，过点B作⊙O的切线，与CA的延长线相交于点D，E是BD的中点，延长AE与CB的延长线相交于点F．
（1）求证：AF是⊙O的切线；
（2）若BE=5，BF=12，求CD的长．

Answer 1

分析 （1）利用直角三角形斜边中线的性质和等边对等角得到∠EAB=∠EBA，结合⊙O的切线得出OA⊥AF，从而得出AF是⊙O的切线；
（2）先根据勾股定理求得EF的长，再根据切线的性质得出EB=EA=5，即可求得AF的长，然后根据切割线定理求得FC，进而得出BC的长，根据E是BD的中点，得出BD的长，最后根据勾股定理即可求得CD的长．

解答 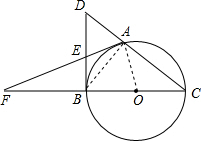解：（1）连接AB，OA，
∵BC是⊙O的直径，
∴∠BAC=90°，
∵DB是⊙O的切线，
∴DB⊥BC，
∴∠DBO=90°，
在RT△ABD中，E是斜边BD的中线，
∴AE=DE=BE，
∴∠EAB=∠EBA，
∵OA=OB，
∴∠OAB=∠OBA，
∴∠EAB+∠OAB=∠EBA+∠OBA
∴∠EAO=∠DBO=90°，
∴OA⊥AF，
∴AF是⊙O的切线；

（2）∵在RT△BEF中，BE=5，BF=12，
∴EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13，
∵FA、DB是⊙O的切线，
∴EA=EB=5，
∴AF=EF+EA=13+5=18，
∵AF²=FB•FC，
∴FC=$\frac{{AF}^{2}}{FB}$=$\frac{1{8}^{2}}{12}$=27，
∴BC=FC-FB=27-12=15，
∵E是BD的中点，
∴BD=2BE=10，
在RT△DBC中，$CD=\sqrt{B{D^2}+B{C^2}}=\sqrt{{{10}^2}+{{15}^2}}=5\sqrt{13}$．

点评 本题考查了切线的判定和性质，直角三角形斜边中线的性质，等腰三角形的性质，勾股定理的应用等，正确的作出辅助线是解题的关键．