
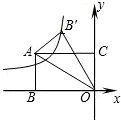
 如图,矩形ABOC在坐标系中,A(-3,
如图,矩形ABOC在坐标系中,A(-3, ),将△ABO沿对角线AO折叠后点B落在B′处,则过点B′的双曲线的解析式为
),将△ABO沿对角线AO折叠后点B落在B′处,则过点B′的双曲线的解析式为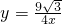
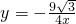
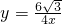
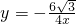
 ),可知OB,OC的长度,利用OB和OC的比值,可求的∠AOB=30°,所以∠AOB′=∠B′OM=30°,过B′点作B′M⊥y轴于M,作B′H⊥x轴于点H,则可求出B′的坐标,进而求出过点B′的双曲线的解析式.
),可知OB,OC的长度,利用OB和OC的比值,可求的∠AOB=30°,所以∠AOB′=∠B′OM=30°,过B′点作B′M⊥y轴于M,作B′H⊥x轴于点H,则可求出B′的坐标,进而求出过点B′的双曲线的解析式.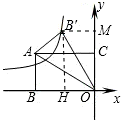 解:过B′点作B′M⊥y轴于M,作B′H⊥x轴于点H,
解:过B′点作B′M⊥y轴于M,作B′H⊥x轴于点H, ),
), ,
,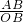 =
= ,
,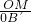 =cos30°,
=cos30°,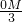 =
= ,
, .
.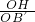 =sin60°,
=sin60°,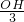 =
= ,
, .
. ,
, ),
), ,
, ×
× =-
=- .
.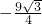 x.
x.

科目:初中数学 来源: 题型:
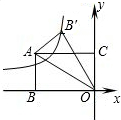 如图,矩形ABOC在坐标系中,A(-3,
如图,矩形ABOC在坐标系中,A(-3,| 3 |
A、y=
| ||||
B、y=-
| ||||
C、y=
| ||||
D、y=-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
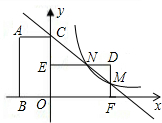 的矩形为DEOF.已知点A的坐标为(-2,m),反比例函数y=
的矩形为DEOF.已知点A的坐标为(-2,m),反比例函数y=| n |
| x |
| n |
| x |
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市十五中中考数学模拟试卷(3月份)(解析版) 题型:解答题
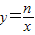 的图象(第一象限)经过线段DF的中点M,且满足m+n=6.
的图象(第一象限)经过线段DF的中点M,且满足m+n=6.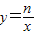 的图象上(写出理由).
的图象上(写出理由).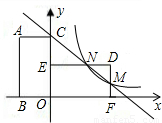
查看答案和解析>>
科目:初中数学 来源:2009年黑龙江省鹤岗市中考数学仿真试卷(三)(解析版) 题型:选择题
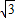 ),将△ABO沿对角线AO折叠后点B落在B′处,则过点B′的双曲线的解析式为( )
),将△ABO沿对角线AO折叠后点B落在B′处,则过点B′的双曲线的解析式为( )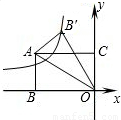
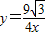
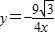
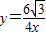
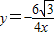
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com