
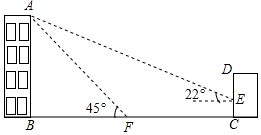
 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).分析 (1)过点E作EM⊥AB于点M,设AB=x,在Rt△ABF中,由∠AFB=45°可知BF=AB=x,在Rt△AEM中,利用锐角三角函数的定义求出x的值即可;
(2)在Rt△AME中,根据cos22°=$\frac{ME}{AE}$可得出结论.
解答 解:(1)如图,过点E作EM⊥AB,垂足为M.
设AB为x.
在Rt△ABF中,∠AFB=45°,
∴BF=AB=x,∴BC=BF+FC=x+25,
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-3,
tan22°=$\frac{AM}{ME}$,
解得:x=23.
即教学楼的高23m.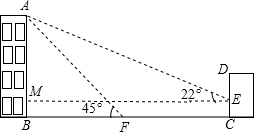
(2)由(1)可得ME=BC=x+27=23+27=50.
在Rt△AME中,cos22°=$\frac{ME}{AE}$.
∴AE=$\frac{ME}{cos22°}$=$\frac{160}{3}$m,
即A、E之间的距离约为$\frac{160}{3}$m.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
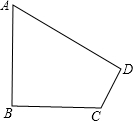 某片绿地的形状如图所示,其中∠A=60°,AB⊥BC,AD⊥CD,AB=200m,CD=100m,
某片绿地的形状如图所示,其中∠A=60°,AB⊥BC,AD⊥CD,AB=200m,CD=100m,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com