练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若化简|1-x|-的结果为2x﹣5，则x的取值范围是（　　）

    A. x为任意实数B. 1≤x≤4 C. x≥1D. x≤4

    【答案】B

    【解析】

    根据完全平方公式先把多项式化简为|1-x|-|x-4|，然后根据x的取值范围分别讨论，求出符合题意的x的值即可．

    原式可化简为|1-x|-|x-4|，

    当1-x≥0，x-4≥0时，可得x无解，不符合题意；

    当1-x≥0，x-4≤0时，可得x≤1时，原式=1-x-4+x=-3；

    当1-x≤0，x-4≥0时，可得x≥4时，原式=x-1-x+4=3；

    当1-x≤0，x-4≤0时，可得1≤x≤4时，原式=x-1-4+x=2x-5，

    据以上分析可得当1≤x≤4时，多项式等于2x-5，

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】本学期实验中学组织开展课外兴趣活动，各活动小班根据实际情况确定了计划组班人数，并发动学生自愿报名，报名人数与计划人数的前5位情况如下：

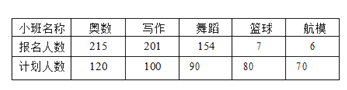
    若用同一小班的计划人数与报名人数的比值大小来衡量进入该班的难易程度，学生中对于进入各活动小班的难易有以下预测：①篮球和航模都能进；②舞蹈比写作容易；③写作比奥数容易；④舞蹈比奥数容易．则预测正确的有___________（填序号即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

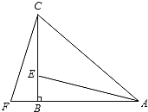
    【题目】如图，在△ABC中，AB=CB，∠BAC=∠BCA，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF.

    (1)求证:Rt△ABE≌ Rt△CBF；

    (2)求证:AE⊥CF；

    (3)若∠CAE=30°，求∠ACF度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场在春节期间搞优惠促销活动，商场将29英寸和25英寸彩电共96台分别以8折和7折出售，共得168400元。已知29英寸彩电原价为3000元/台，25英寸彩电原价为2000元/台，出售29英寸和25英寸彩电各多少台？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

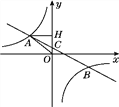
    【题目】【题目】如图，在平面直角坐标系中，一次函数y＝ax＋b(a≠0)的图象与反比例函数y＝ (k≠0)的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH＝3，tan∠AOH＝，点B的坐标为(m，－2)．

    (1)求△AHO的周长；

    (2)求该反比例函数和一次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以圆O为圆心，半径为1的弧交坐标轴于A，B两点，P是弧上一点（不与A，B重合），连接OP，设∠POB=α，则点P的坐标是

    A. （sinα，sinα） B. （cosα，cosα） C. （cosα，sinα） D. （sinα，cosα）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知平行四边形ABCD顶点A的坐标为（2，6），点B在y轴上，且AD∥BC∥x轴，过B，C，D三点的抛物线y=ax2+bx+c（a≠0）的顶点坐标为（2，2），点F（m，6）是线段AD上一动点，直线OF交BC于点E．

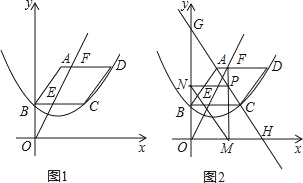
    （1）求抛物线的表达式；

    （2）设四边形ABEF的面积为S，请求出S与m的函数关系式，并写出自变量m的取值范围；

    （3）如图2，过点F作FM⊥x轴，垂足为M，交直线AC于P，过点P作PN⊥y轴，垂足为N，连接MN，直线AC分别交x轴，y轴于点H，G，试求线段MN的最小值，并直接写出此时m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，可以单独用正三角形、正方形或正六边形铺满地面，如果我们要同时用两种不同的正多边形铺满地面，可以设计出几种不同的组合方案？

    问题解决：

    猜想1：是否可以同时用正方形、正八边形两种正多边形组合铺满地面？

    验证1并完成填空：在铺地面时，设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意：可得方程①： ，

    整理得②： ，

    我们可以找到方程的正整数解为③： ．

    结论1：铺满地面时，在一个顶点周围围绕着④个正方形和⑤个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以铺满地面．

    猜想2：是否可以同时用正三角形和正六边形两种正多边形组合铺满地面？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案